BA Marvin Henke
Auflösungseffekte in Modellen verschiedener Reynolds-Regime für Unterschallströmungen um ein Hindernis
Herleitung inkompressible,inviskose, wirbelfreie Strömung um einen Zylinder
Betrachtet wird ein sich mit Geschwindigkeit \(\vec{v_0}=v_0 \hat{x}\) durch ein Fluid bewegender Zylinder mit Radius \(R\). Es wird in Zylinderkoordinaten \((r,\varphi,z)\) gerechnet, wobei die \(z\)-Dimension irrelevant für die Rechnung ist. Aufgrund der Annahmen (inkompressibel, inviskos, wirbelfrei) gilt folgendes: \begin{align} \frac{\mathrm{d} \rho}{\mathrm{d} t} = 0\ ,\ \frac{\partial \rho}{\partial t} + \vec{\nabla}\cdot(\rho\vec{v}) = \frac{\partial \rho}{\partial t} + \vec{u}\cdot\vec{\nabla}\rho + \rho(\vec{\nabla}\cdot\vec{v}) = \frac{\mathrm{d} \rho}{\mathrm{d} t} + \rho (\vec{\nabla}\cdot\vec{v}) = 0 \ \Rightarrow\ \vec{\nabla}\cdot\vec{v}=0\\ \vec{\nabla}\times\vec{v}=0 \ \Rightarrow\ \exists \phi : \vec{v} = \vec{\nabla} \phi \end{align} Daher folgt aus der Annahme \(\frac{\mathrm{d}\rho}{\mathrm{d}t}=0\) mit der Kontinuitätsgleichung, dass \(\vec{\nabla}\cdot\vec{u}=0\) gelten muss, also die Divergenzfreiheit des Geschwindigkeitsfelds.
Für das Potential \(\phi\) folgt Aufgrund von \(\vec{\nabla}\cdot\vec{v}=0\), dass \(\Delta\phi = 0\) gilt (Laplace-Gleichung).
Im Unendlichen soll die Geschwindigkeit des Fluids verschwinden, d.h. \( \vec{v} \xrightarrow[]{r \to \infty} \vec{0}\).
Für den Rand des Zylinders soll die Relativgeschwindigkeit des Fluids senkrecht zur Oberflächennormale sein, d.h. \(\forall \varphi : (\vec{v}(r=R,\varphi) - v_0 \hat{x})\cdot \hat{n} = 0 \).
Es ist also eine Lösung der Laplace-Gleichung auf \( \mathbb{R}^2 \setminus B_R(0) \) gesucht, welche im Unendlichen einen verschwindenden Gradienten hat und auf \( \partial B_R(0) \) die Neumann-Randbedingung \( \partial_n \phi = v_0 \hat{n}\cdot\hat{x} \) erfüllt. Die Fundamentallösungen der Laplace-Gleichung inspirieren folgenden Ansatz: \begin{align} \phi(r,\varphi) = \frac{c(\varphi)}{r} \end{align} Für beschränkte \( c(\varphi) \) verschwindet das Potential und die Geschwindigkeit im Unendlichen. Einsetzen in die Laplace-Gleichung liefert die folgende Bedingung an \( c(\varphi) \): \begin{align} c^{\prime\prime}(\varphi) + c(\varphi) = 0 \ \Rightarrow\ c(\varphi) = A \sin (\varphi) + B \cos (\varphi) \end{align}
Durch die Neumann-Bedingung lassen sich die Koeffizienten bestimmen: \(A = 0\) und \(B=-v_0 R^2\)
Damit ist das gesuchte Potential gefunden: \begin{align} \phi(r,\varphi) = -v_0 R^2 \frac{\cos \varphi}{r} \end{align} Es ergibt sich folgende Flussgeschwindigkeit als Gradient des Potentials: \begin{align} \vec{\nabla}\phi = \vec{v}(r,\varphi) = \frac{R^2}{r^2} v_0 \left[ \hat{r} \cos\varphi + \hat{\varphi} \sin\varphi \right] \end{align}
Für die Flussgeschwindigkeit um einen umströmten statischen Zylinder, wird nun die Geschwindigkeit des bewegten Zylinders subtrahiert. Es ergibt sich: \begin{align} \vec{v}(r,\varphi) = \frac{R^2}{r^2} v_0 \left[ \hat{r} \cos\varphi + \hat{\varphi} \sin\varphi \right] - v_0 \hat{x}\\ \vec{v}(r,\varphi) = \frac{R^2}{r^2} v_0 \left[ \hat{r} \cos\varphi + \hat{\varphi} \sin\varphi \right] - v_0 (\hat{r} \cos\varphi - \hat{\varphi} \sin\varphi)\\ \vec{v}(r,\varphi) = v_0 \left[ \hat{r} (\frac{R^2}{r^2} - 1) \cos\varphi + \hat{\varphi} (\frac{R^2}{r^2} + 1) \sin\varphi \right] \end{align}
Für den Druck lässt sich mit der Bernoulli-Gleichung \(\displaystyle \frac{v^2}{2} + \frac{p}{\rho} = \mathrm{const.}\) folgender Ausdruck herleiten: \begin{align} p=\frac{\rho}{2}v_0^2\left(2\frac{R^2}{r^2}\cos2\varphi-\frac{R^4}{r^4}\right) \end{align}
Stabilitätsanalyse
Es soll nun eine Stabilitätsanalyse für die inkompressible Strömung (mit \(\rho(x,t) = \rho_0\)) um den Zylinder bei einer Reynoldszahl im Übergangsbereich Krichregime \(\rightarrow\) Vortexregime oder Vortexregime \(\rightarrow\) laminar periodisch durchgeführt werden. Die zugrunde liegenden Gleichungen in dem Satz natürlicher Einheiten (\(\rho_0\), \(v_0\), \(D\)) mit \(\mathrm{Re}=\frac{\rho_0 v_0 D}{\mu}\)sind: \begin{align} \vec{\nabla} \cdot \vec{v} &= 0 \\ \partial_t \vec{v} + (\vec{v} \cdot \vec{\nabla})\vec{v} + \vec{\nabla} p - \frac{1}{\mathrm{Re}}\Delta \vec{v} &= 0 \end{align} Angenommen man hat eine Lösung (\(\vec{v}, p\)) dieser Gleichungen für eine Reynoldszahl \(\mathrm{Re}=:a\) und stört diese mit (\(\delta \vec{v}\), \(\delta p\)). Die Frage ist nun, wie sich diese Störungen in erster Ordnung verhalten, wenn wir die gestörte Lösung in die Kontinuitätsgleichung & Impulsgleichung für eine andere Reynoldszahl \(\mathrm{Re}=:b\) einsetzen.
Aus der Kontinuitätsgleichung wird einfach eine Kontinuitätsgleichung für die Störung: \begin{align} \vec{\nabla} \cdot \delta\vec{v} = 0 \end{align} Die linearisierte Impulsgleichung für (\(\vec{v}+\delta\vec{v}\), \(p+\delta p\)) bei \(\mathrm{Re}=b\) ist die folgende: \begin{align} \left(\frac{b-a}{a b}\right)\Delta \vec{v} + (\delta\vec{v}\cdot\vec{\nabla})\vec{v} + (\vec{v}\cdot\vec{\nabla})\delta\vec{v} + \vec{\nabla}\delta p + \partial_t \delta\vec{v} - \frac{1}{b}\Delta\delta\vec{v} = 0 \end{align} Man wählt nun einen Exponentialansatz für die Störung (aufgrund der Linearität der Gleichungen): \begin{align} \delta\vec{v} &= \delta\vec{v_0} \exp\left(i(\vec{k}\cdot\vec{r} - \omega t)\right)\\ \delta p &= \delta p_0 \exp\left(i(\vec{k}\cdot\vec{r} - \omega t)\right) \end{align} Es gelten nun folgende Gleichungen: \begin{align} \vec{\nabla}\delta p &= i \vec{k}\delta p\\ \partial_t \delta\vec{v} &= -i \omega \delta\vec{v}\\ \Delta\delta\vec{v} &= - k^2 \delta\vec{v}\\ (\vec{v}\cdot\vec{\nabla})\delta\vec{v} &= i (\vec{v}\cdot\vec{k})\delta\vec{v} \end{align} Damit wird die Kontinuitätsgleichung und Impulsgleichung zu: \begin{align} \vec{k} \cdot \delta\vec{v} = 0\\ \left(\frac{b-a}{a b}\right)\Delta \vec{v} + (\delta\vec{v}\cdot\vec{\nabla})\vec{v} + i (\vec{v}\cdot\vec{k})\delta\vec{v} + i\vec{k}\delta p - i \omega \delta\vec{v} + \frac{1}{b}k^2\delta\vec{v} = 0 \end{align}
Für \(a = b\) fällt der erste Term weg.
Da die Störungen nicht die Randbedingungen erfüllen, gibt es bessere Ansätze. Einer wären z.B. Besselfunktionen. Als analytische Lösung für den ersten Übergang könnte man die Lösung der Potentialströmung verwenden.
In Zylinderkoordinaten lauten die linearisierten Gleichungen für eine beliebige Störung: \begin{align} \frac{1}{r} \left(\partial_r(r \delta v_r) + \partial_{\varphi}(\delta v_{\varphi})\right) &= 0\\ \delta v_r \partial_r v_r + \frac{\delta v_{\varphi}}{r} \partial_{\varphi} v_r + v_r \partial_r \delta v_r + \frac{v_{\varphi}}{r}\partial_{\varphi} \delta v_r - 2 \frac{v_{\varphi} \delta v_{\varphi}}{r} + \partial_r \delta p - \frac{1}{b} \left(\frac{1}{r}\partial_r(r \partial_r \delta v_r) + \frac{1}{r^2}\partial_{\varphi}^2 \delta v_r - \frac{1}{r^2}\delta v_r - \frac{2}{r^2} \partial_{\varphi} \delta v_{\varphi} \right) &= \partial_t \delta v_r\\ \delta v_r \partial_r v_{\varphi} + \frac{\delta v_{\varphi}}{r} \partial_{\varphi} v_{\varphi} + v_r \partial_r \delta v_{\varphi} + \frac{v_{\varphi}}{r}\partial_{\varphi} \delta v_{\varphi} + 2 \frac{v_{\varphi} \delta v_r}{r} + \frac{1}{r} \partial_{\varphi} \delta p - \frac{1}{b} \left(\frac{1}{r}\partial_r(r \partial_r \delta v_{\varphi}) + \frac{1}{r^2}\partial_{\varphi}^2 \delta v_{\varphi} - \frac{1}{r^2}\delta v_{\varphi} + \frac{2}{r^2} \partial_{\varphi} \delta v_r \right) &= \partial_t \delta v_{\varphi} \end{align}
Numerik und Simulationsparameter
Die Simulation läuft in Zylinderkoordinaten, der Radius des Zylinders beträgt \(R = 1\), der Radius des Simulationsgebiets beträgt \(R_{\infty}=10\) (bzw. für spätere Simulationen \(R_{\infty}=100\)).
Die externe Einströmgeschwindigkeit wird über die Mach-Zahl \(\mathcal{M}=\frac{v_{\mathrm{ext}}}{c}\) geregelt, die Reynoldszahl \(\mathrm{Re} = \frac{v L}{\nu}\) regelt die kinematische Viskosität \(\nu\).
Die externe Dichte \(\rho_{\mathrm{ext}}\) wird auf \(1\) normiert, genauso die Schallgeschwindigkeit \(c\).
Mit \(p V^{\gamma} = \mathrm{const.}\) und \(c^2 = \left(\frac{\partial p}{\partial\rho}\right)_S\) folgt für den externen Druck \(p_{\mathrm{ext}} = \frac{c^2 \rho_{\mathrm{ext}}}{\gamma}\) , wobei \(\gamma\) der Isentropenexponent \(\gamma = 1 + \frac{2}{f}\) mit der Anzahl an Freiheitsgraden \(f\) ist.
Die Anfangsbedingungen sind folgende: \begin{align} \vec{v}_0 = -v_{\mathrm{ext}} \hat{x}\\ \rho_0 = \rho_{\mathrm{ext}} = 1\\ p_0 = p_{\mathrm{ext}} \end{align}
Für die Winkel sind periodische Randbedingungen definiert, in radiale Richtung werden für die Zylinderoberfläche reflektive Randbedingungen verwendet. In \(z\)-Richtung werden outflow-Randbedingungen benutzt.
In radiale Richtung auf dem äußeren Rand des Simulationsgebiets sind die Randbedingungen benutzerdefiniert. Standardmäßig wird hier \(\rho = \rho_{\mathrm{ext}}\), \(\vec{v} = \vec{v}_0\) und \(p = p_{\mathrm{ext}}\) für die Geisterzellen verwendet. Verwendet man outflow/inflow Randbedingungen für \(x < 0\) erzielt man minimal bessere Ergebnisse. Hierfür wurde die selbe Simulation für \(R_{\infty} = 100\) durchgeführt. Vergleicht man nun das Dichtefeld aus dieser Simulation (hier sind aufgrund des großen Radius die Randbedingungen nahezu beliebig) mit dem Dichtefeld für konstante Randbedingungen bzw. outflow/inflow Randbegingungen, so stellt sich heraus, dass die outflow/inflow Randbedingung zu kleineren Abweichungen führt. Mit outflow/inflow Randbedingungen ist gemeint, dass das Geschwindigkeitsfeld am Rand in die Geisterzellen fortgesetzt wird, während die Dichte und der Druck wie zuvor konstant auf einen Randwert festgesetzt werden.
Da diese Verbesserungen allerdings sehr klein ist, wurden alle weiteren Simulationen weiterhin mit konstanten Randbedingungen durchgeführt, um Konsistenz mit den vorherigen Simulationen zu garantieren.
Bestimmung der Regimeübergänge
Im folgenden sollen die Reynoldszahlen der Übergänge verschiedener Strömungsregime bestimmt werden. Da die Strömungskenngrößen (\(z.B. \rho, \vec{v}\)) aufgrund der Numerik diskret sind, helfen folgende Definitionen für Skalarfelder: \begin{align} t = k\Delta t \ \ \Rightarrow s(\vec{x},t)\ \widehat{=}\ s_i^k \\ \dot{s}_i^{k+\frac{n}{2}}\ \widehat{=}\ \frac{s_i^{k+n} - s_i^k}{n\Delta t} \end{align} Außerdem sei \(\Delta t_k\) die \(k\)-te Zeitschrittweite und \(\Delta V_i\) das Volumen der \(i\)-ten Zelle. Im Folgenden wird über Zeitintervalle und Volumina summiert, dafür gilt \(T = \sum_k \Delta t_k\) und \( V = \sum_i \Delta V_i \).
Methodik zur Bestimmung des Übergangs von L1 in L2
Im Folgenden ist die implementierte Methodik zur Bestimmung des ersten Übergangs von L1 (creeping flow / non-separation regime [0 < RE < 4-5]) zu L2 (closed near-wake regime [4-5 < RE < 30-48]) beschrieben. Der wesentliche Unterschied liegt in der Symmetrie des Flusses bezüglich der y-Achse. Für L1 ist eine hohe Symmetrie zu erwarten, während für L2 aufgrund der sich bildenden Vortices hinter dem Zylinder eine niedrigere Symmetrie zu erwarten ist. Als Maß für die Symmetrie eines Skalarfelds \(s\) (z.B. \(\rho\)) wird folgende Definition verwendet: \begin{align} \mathcal{S}[s(r,\varphi)] := 1 - \frac{\int d^2(r,\varphi^*) \mathrm{d}r \mathrm{d}\varphi^*}{\int s^2(r,\varphi) \mathrm{d}r \mathrm{d}\varphi}\\ d(r,\varphi) := s(r,\varphi) - s(r,\pi-\varphi) %\mathcal{S}(s) := 1-\left\langle\frac{\left\langle \left( s(r,\varphi^*,t) - s(r,\pi-\varphi^*,t) \right)^2 \right\rangle_{r,\varphi^*}}{\left\langle s^2(r,\varphi,t) \right\rangle_{r,\varphi}}\right\rangle_t = 1-\frac{1}{T} \sum_k \frac{\Delta t_k}{\sum_i \Delta V_i (s_i^k)^2} %\sum_{-\frac{\pi}{2} < \varphi < \frac{\pi}{2}} \Delta V(\varphi) \left[s^k(\varphi) - s^k(\pi - \varphi) \right]^2 \end{align} Hierbei gilt \(\varphi^* \in (-\pi/2, \pi/2)\) und \(\varphi \in (0,2\pi)\).
Diese Definition von \(\mathcal{S}(s)\) garantiert, dass für Skalarfelder \(s(x,y) = -s(-x,y)\) die Symmetrie \(\mathcal{S}(s) = -1\) beträgt. Anderesherum gilt für ein Skalarfeld mit \(s(x,y)=s(-x,y)\), dass \(\mathcal{S}(s) = 1\) gilt. Aufgrund der Normierung hat \(\mathcal{S}(s)\) immer die Dimension Zahl.
Alternativ kann die Rotation betrachtet werden. Diese sollte aufgrund der Wirbel in L2 größer sein. Als Maß der Rotation eines Vektorfelds \(\vec{f}\) (z.B. \(\vec{v}\)) wird folgende Definition verwendet: \begin{align} \mathcal{R}(\vec{f}) := \frac{L}{f_{\mathrm{ext}}} \left\langle \left(\vec{\nabla}\times\vec{f}\right)_z \right\rangle_{r,\varphi} \end{align} Hierbei wird der Erwartungswert nur über die obere Hälfte \(0<\varphi<\pi\) gebildet.
Methodik zur Bestimmung des Übergangs von L2 in L3
Beim Übergang von L2 (closed near-wake regime [4-5 < RE < 30-48]) zu L3 (periodic laminar regime [30-48 < RE < 180-200]) ändert sich das Verhalten des Systems im steady state. In L2 wird nach einiger Zeit ein zeitlich konstanter steady state angenommen, in L3 hingegen verhält sich das System periodisch, d.h. man müsste den Übergang anhand der Zeitableitung der Strömungskenngrößen erkennen können. Dazu wird folgende Größe definiert: \begin{align}\mathcal{C}_t(s,n) := \frac{\left\langle \left( \frac{\partial}{\partial t} s(r,\varphi,t) \right)^2 \right\rangle_{r,\varphi,t}}{\left(\frac{v_{\mathrm{ext}}}{L}\right)^2 \left\langle s^2(r,\varphi,t) \right\rangle_{r,\varphi,t}} = \frac{\sum_{i, k} \Delta t_k \Delta V_i {(\dot{s}_i^{k+\frac{n}{2}})}^2}{\left(\frac{v_{\mathrm{ext}}}{L}\right)^2 \sum_{i, k} \Delta t_k \Delta V_i {(s_i^{k})}^2} \end{align} Prinzipiell handelt es sich hier um den Erwartungswert bezüglich Zeit und Ort der Größe \({(\dot{s}_i^{k+\frac{n}{2}})}^2\). Das \(n\) gibt an wie viele Mittelungen bei der Berechnung des diskreten Differenzenquotienten gemacht werden. Aufgrund der Normierung hat \(\mathcal{C}_t(s,n)\) immer die Dimension Zahl.
Simulationsergebnisse
Interpretation
Symmetrie \(\mathcal{S}\)
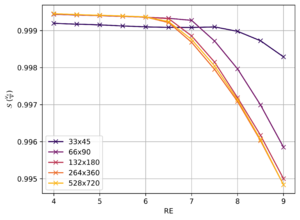
Die Symmetrie \(\mathcal{S}\) zeigt für \(\vec{v}\) einen stetigen Übergang von L1 in L2. Daher wurde zusätzlich die Rotation betrachtet. Hierbei ist dasselbe aufgefallen, weshalb die normierte Geschwindigkeit betrachtet wurde. Für die normierte Geschwindigkeiten \(v_x/v\) und \(v_y/v\) weißt die Symmetrie \(\mathcal{S}\) einen Knick bei \(\mathrm{Re}\approx 6\) auf.
Rotation \(\mathcal{R}\)
Die reine Rotation ist beim Übergang von L1 nach L2 auch stetig, allerdings weißt die Rotation des normierten Vektorfelds eine klare Kante auf. Ab einem Bestimmten Punkt entstehen also Wirbel. Um herauszufinden, ob dieser Punkt von der Auflösung des Gitters abhängt, sollten mehrere Gitterauflösungen betrachtet werden. Es wäre durchaus möglich, dass der Sprung nur entsteht, weil die Wirbel erst ab einer Bestimmten Größe (ca. 2 Gitterzellen) vom Gitter aufgelöst werden können. Wie die Abbildungen zeigen, ist dies nicht der Fall, es gibt also eine inhärente minimale Wirbelgröße. Die ersten Wirbel entstehen bei \(\mathrm{Re}=6 \rightarrow \mathrm{Re}=6.5\).
Der Übergang von L1 in L2 scheint also bei etwa \(\mathrm{Re}=6\) stattzufinden.
Zeitableitung \(\mathcal{C}_t\)
Für einen kleinen Außenradius (\(R_{\infty}=10\)) scheint der Übergang durch \(\mathrm{Re}=60\) markiert zu sein, dies ist allerdings scheinbar durch Randeffekte bedingt, da der Übergang für \(R_{\infty}=100\) schon früher stattfindet. Dies wäre auch in besserer Übereinstimmung mit der Literatur, welche einen Übergang bei \(30 < \mathrm{Re} < 48\) angibt. Um hier den Übergangsbereich zu untersuchen, läuft gerade eine Simulation mit mit \(R_{\infty}=100\) für kleinere Reynoldszahlen.