BA Marvin Henke

Auflösungseffekte in Modellen verschiedener Reynolds-Regime für Unterschallströmungen um ein Hindernis

Herleitung inkompressible,inviskose, wirbelfreie Strömung um einen Zylinder

Betrachtet wird ein sich mit Geschwindigkeit $\overrightarrow{v_0}=v_0\hat{x}$ durch ein Fluid bewegender Zylinder mit Radius $R$. Es wird in Zylinderkoordinaten $(r,\phi ,z)$ gerechnet, wobei die $z$-Dimension irrelevant für die Rechnung ist. Aufgrund der Annahmen (inkompressibel, inviskos, wirbelfrei) gilt folgendes: $$\begin{array}{r}\frac{\mathrm{d}\rho }{\mathrm{d}t}=0,\frac{\partial \rho }{\partial t}+\overrightarrow{\mathrm{\nabla }}\cdot (\rho \overrightarrow{v})=\frac{\mathrm{d}\rho }{\mathrm{d}t}+\rho (\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{v})=0\Rightarrow \overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{v}=0\\ \overrightarrow{\mathrm{\nabla }}\times \overrightarrow{v}=0\Rightarrow \mathrm{\exists }\varphi :\overrightarrow{v}=\overrightarrow{\mathrm{\nabla }}\varphi \end{array}$$ Für das Potential $\varphi$ folgt Aufgrund von $\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{v}=0$, dass $\mathrm{\Delta }\varphi =0$ gilt (Laplace-Gleichung).

Im Unendlichen soll die Geschwindigkeit des Fluids verschwinden, d.h. $\overrightarrow{v}\stackrel{r\to \mathrm{\infty }}{\to }\overrightarrow{0}$.

Für den Rand des Zylinders soll die Relativgeschwindigkeit des Fluids senkrecht zur Oberflächennormale sein, d.h. $\mathrm{\forall }\phi :(\overrightarrow{v}(r=R,\phi )-v_0\hat{x})\cdot \hat{n}=0$.

Es ist also eine Lösung der Laplace-Gleichung auf ${\mathbb{R}}^2\setminus B_R(0)$ gesucht, welche im Unendlichen einen verschwindenden Gradienten hat und auf $\partial B_R(0)$ die Neumann-Randbedingung ${\partial }_n\varphi =v_0\hat{n}\cdot \hat{x}$ erfüllt. Die Fundamentallösungen der Laplace-Gleichung inspirieren folgenden Ansatz: $$\begin{array}{r}\varphi (r,\phi )=\frac{c(\phi )}{r}\end{array}$$ Für beschränkte $c(\phi )$ verschwindet das Potential und die Geschwindigkeit im Unendlichen. Einsetzen in die Laplace-Gleichung liefert die folgende Bedingung an $c(\phi )$: $$\begin{array}{r}{c}^{\prime \prime }(\phi )+c(\phi )=0\Rightarrow c(\phi )=A\sin (\phi )+B\cos (\phi )\end{array}$$

Durch die Neumann-Bedingung lassen sich die Koeffizienten bestimmen: $A=0$ und $B=-v_0{R}^2$

Damit ist das gesuchte Potential gefunden: $$\begin{array}{r}\varphi (r,\phi )=-v_0{R}^2\frac{\cos \phi }{r}\end{array}$$ Es ergibt sich folgende Flussgeschwindigkeit als Gradient des Potentials: $$\begin{array}{r}\overrightarrow{\mathrm{\nabla }}\varphi =\overrightarrow{v}(r,\phi )=\frac{R^2}{r^2}{v}_0[\hat{r}\cos \phi +\hat{\phi }\sin \phi ]\end{array}$$

Für die Flussgeschwindigkeit um einen umströmten statischen Zylinder, wird nun die Geschwindigkeit des bewegten Zylinders subtrahiert. Es ergibt sich: $$\begin{array}{r}\overrightarrow{v}(r,\phi )=\frac{R^2}{r^2}{v}_0[\hat{r}\cos \phi +\hat{\phi }\sin \phi ]-v_0\hat{x}\\ \overrightarrow{v}(r,\phi )=\frac{R^2}{r^2}{v}_0[\hat{r}\cos \phi +\hat{\phi }\sin \phi ]-v_0(\hat{r}\cos \phi -\hat{\phi }\sin \phi )\\ \overrightarrow{v}(r,\phi )=v_0[\hat{r}(\frac{R^2}{r^2}-1)\cos \phi +\hat{\phi }(\frac{R^2}{r^2}+1)\sin \phi ]\end{array}$$

Für den Druck lässt sich mit der Bernoulli-Gleichung $\frac{v^2}{2}+\frac{p}{\rho }=\mathrm{const}.$ folgender Ausdruck herleiten: $$\begin{array}{r}p=\frac{\rho }{2}{v}_0^2(2\frac{R^2}{r^2}\cos 2\phi -\frac{R^4}{r^4})\end{array}$$

Stabilitätsanalyse

Es soll nun eine Stabilitätsanalyse für die inkompressible Strömung (mit $\rho (x,t)={\rho }_0$) um den Zylinder bei einer Reynoldszahl im Übergangsbereich Krichregime $\to$ Vortexregime oder Vortexregime $\to$ laminar periodisch durchgeführt werden. Die zugrunde liegenden Gleichungen in dem Satz natürlicher Einheiten (${\rho }_0$, $v_0$, $D$) mit $\mathrm{Re}=\frac{{\rho }_0{v}_{0}D}{\mu }$sind: $$\begin{array}{rl}\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{v}& =0\\ {\partial }_t\overrightarrow{v}+(\overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{v}+\overrightarrow{\mathrm{\nabla }}p-\frac{1}{\mathrm{Re}}\mathrm{\Delta }\overrightarrow{v}& =0\end{array}$$ Angenommen man hat eine Lösung ($\overrightarrow{v},p$) dieser Gleichungen für eine Reynoldszahl $\mathrm{Re}=:a$ und stört diese mit ($\delta \overrightarrow{v}$, $\delta p$). Die Frage ist nun, wie sich diese Störungen in erster Ordnung verhalten, wenn wir die gestörte Lösung in die Kontinuitätsgleichung & Impulsgleichung für eine andere Reynoldszahl $\mathrm{Re}=:b$ einsetzen.

Aus der Kontinuitätsgleichung wird einfach eine Kontinuitätsgleichung für die Störung: $$\begin{array}{r}\overrightarrow{\mathrm{\nabla }}\cdot \delta \overrightarrow{v}=0\end{array}$$ Die linearisierte Impulsgleichung für ($\overrightarrow{v}+\delta \overrightarrow{v}$, $p+\delta p$) bei $\mathrm{Re}=b$ ist die folgende: $$\begin{array}{r}\left(\frac{b-a}{ab}\right)\mathrm{\Delta }\overrightarrow{v}+(\delta \overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{v}+(\overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }})\delta \overrightarrow{v}+\overrightarrow{\mathrm{\nabla }}\delta p+{\partial }_t\delta \overrightarrow{v}-\frac{1}{b}\mathrm{\Delta }\delta \overrightarrow{v}=0\end{array}$$ Man wählt nun einen Exponentialansatz für die Störung (aufgrund der Linearität der Gleichungen): $$\begin{array}{rl}\delta \overrightarrow{v}& =\delta \overrightarrow{v_0}\exp (i(\overrightarrow{k}\cdot \overrightarrow{r}-\omega t))\\ \delta p& =\delta p_0\exp (i(\overrightarrow{k}\cdot \overrightarrow{r}-\omega t))\end{array}$$ Es gelten nun folgende Gleichungen: $$\begin{array}{rl}\overrightarrow{\mathrm{\nabla }}\delta p& =i\overrightarrow{k}\delta p\\ {\partial }_t\delta \overrightarrow{v}& =-i\omega \delta \overrightarrow{v}\\ \mathrm{\Delta }\delta \overrightarrow{v}& =-k^2\delta \overrightarrow{v}\\ (\overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }})\delta \overrightarrow{v}& =i(\overrightarrow{v}\cdot \overrightarrow{k})\delta \overrightarrow{v}\end{array}$$ Damit wird die Kontinuitätsgleichung und Impulsgleichung zu: $$\begin{array}{r}\overrightarrow{k}\cdot \delta \overrightarrow{v}=0\\ \left(\frac{b-a}{ab}\right)\mathrm{\Delta }\overrightarrow{v}+(\delta \overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{v}+i(\overrightarrow{v}\cdot \overrightarrow{k})\delta \overrightarrow{v}+i\overrightarrow{k}\delta p-i\omega \delta \overrightarrow{v}+\frac{1}{b}{k}^2\delta \overrightarrow{v}=0\end{array}$$

Bis hier hin sind keinerlei Randbedingungen eingeflossen. Da diese aber notwendig für eine eindeutige Lösung sind, müssen sie natürlich auch betrachtet werden. D.h. am Zylinderrand muss $\overrightarrow{v}=\overrightarrow{0}$ gelten. In der Impulsgleichung stehen nun auch Ableitungen von $\overrightarrow{v}$, um diese zu berücksichtigen, wird eine Taylorentwicklung zweiter Ordnung im Radius gemacht: $$\begin{array}{r}\overrightarrow{v}(r,\phi )\approx \frac{\partial \overrightarrow{v}}{\partial r}{|}_{r=R}(r-R)+\frac{{\partial }^2\overrightarrow{v}}{\partial r^2}{|}_{r=R}\frac{(r-R{)}^2}{2}\end{array}$$ Hiermit ergeben sich folgende Terme in Zylinderkoordinaten: $$\begin{array}{rl}\mathrm{\Delta }\overrightarrow{v}{|}_{r=R}& =\frac{1}{R}\frac{\partial \overrightarrow{v}}{\partial r}{|}_{r=R}+\frac{{\partial }^2\overrightarrow{v}}{\partial r^2}{|}_{r=R}\\ (\delta \overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{v}{|}_{r=R}& =\delta v_r\frac{\partial \overrightarrow{v}}{\partial r}{|}_{r=R}\end{array}$$ Einsetzen in die Impulsgleichung für $r=R$ liefert: $$\begin{array}{r}\frac{b-a}{ab}(\frac{1}{R}\frac{\partial \overrightarrow{v}}{\partial r}+\frac{{\partial }^2\overrightarrow{v}}{\partial r^2})+\delta v_r\frac{\partial \overrightarrow{v}}{\partial r}+i\overrightarrow{k}\delta p-i\omega \delta \overrightarrow{v}+\frac{k^2}{b}\delta \overrightarrow{v}=0\end{array}$$ Von Interesse ist nun der Imaginärteil von $\omega$, da dieser das zeitliche Verhalten bestimmt. Für $\mathrm{Im}(\omega )>0$ ist die Lösung instabil und die Störung steigt exponentiell an. Für $\mathrm{Im}(\omega )<0$ hingegen verschwindet die Störung mit der Zeit.

Der einzige Term, der $\omega$ enthält, zeigt in Richtung $\delta \overrightarrow{v}$. Da $\overrightarrow{k}$ senkrecht auf $\delta \overrightarrow{v}$ steht, lässt sich die Impulsgleichung durch Multiplikation mit $\delta \overrightarrow{v}$ umschreiben: $$\begin{array}{r}\frac{b-a}{ab}(\frac{1}{R}\frac{\partial \overrightarrow{v}}{\partial r}\cdot \delta \overrightarrow{v}+\frac{{\partial }^2\overrightarrow{v}}{\partial r^2}\cdot \delta \overrightarrow{v})+\delta v_r\frac{\partial \overrightarrow{v}}{\partial r}\cdot \delta \overrightarrow{v}+\frac{k^2}{b}\delta {\overrightarrow{v}}^2=i\omega \delta {\overrightarrow{v}}^2\end{array}$$

Numerik und Simulationsparameter

Die Simulation läuft in Zylinderkoordinaten, der Radius des Zylinders beträgt $R=1$, der Radius des Simulationsgebiets beträgt $R_{\mathrm{\infty }}=10$ (bzw. für spätere Simulationen $R_{\mathrm{\infty }}=100$).

Die externe Einströmgeschwindigkeit wird über die Mach-Zahl $\mathcal{M}=\frac{v_{\mathrm{ext}}}{c}$ geregelt, die Reynoldszahl $\mathrm{Re}=\frac{vL}{\nu }$ regelt die kinematische Viskosität $\nu$.

Die externe Dichte ${\rho }_{\mathrm{ext}}$ wird auf $1$ normiert, genauso die Schallgeschwindigkeit $c$.

Mit $p{V}^{\gamma }=\mathrm{const}.$ und $c^2={\left(\frac{\partial p}{\partial \rho }\right)}_S$ folgt für den externen Druck $p_{\mathrm{ext}}=\frac{c^2{\rho }_{\mathrm{ext}}}{\gamma }$ , wobei $\gamma$ der Isentropenexponent $\gamma =1+\frac{2}{f}$ mit der Anzahl an Freiheitsgraden $f$ ist.

Die Anfangsbedingungen sind folgende: $$\begin{array}{r}{\overrightarrow{v}}_0=-v_{\mathrm{ext}}\hat{x}\\ {\rho }_0={\rho }_{\mathrm{ext}}=1\\ p_0=p_{\mathrm{ext}}\end{array}$$

Für die Winkel sind periodische Randbedingungen definiert, in radiale Richtung werden für die Zylinderoberfläche reflektive Randbedingungen verwendet. In $z$-Richtung werden outflow-Randbedingungen benutzt.

In radiale Richtung auf dem äußeren Rand des Simulationsgebiets sind die Randbedingungen benutzerdefiniert. Standardmäßig wird hier $\rho ={\rho }_{\mathrm{ext}}$, $\overrightarrow{v}={\overrightarrow{v}}_0$ und $p=p_{\mathrm{ext}}$ für die Geisterzellen verwendet. Verwendet man outflow/inflow Randbedingungen für $x<0$ erzielt man minimal bessere Ergebnisse. Hierfür wurde die selbe Simulation für $R_{\mathrm{\infty }}=100$ durchgeführt. Vergleicht man nun das Dichtefeld aus dieser Simulation (hier sind aufgrund des großen Radius die Randbedingungen nahezu beliebig) mit dem Dichtefeld für konstante Randbedingungen bzw. outflow/inflow Randbegingungen, so stellt sich heraus, dass die outflow/inflow Randbedingung zu kleineren Abweichungen führt. Mit outflow/inflow Randbedingungen ist gemeint, dass das Geschwindigkeitsfeld am Rand in die Geisterzellen fortgesetzt wird, während die Dichte und der Druck wie zuvor konstant auf einen Randwert festgesetzt werden.

Da diese Verbesserungen allerdings sehr klein ist, wurden alle weiteren Simulationen weiterhin mit konstanten Randbedingungen durchgeführt, um Konsistenz mit den vorherigen Simulationen zu garantieren.

Bestimmung der Regimeübergänge

Im folgenden sollen die Reynoldszahlen der Übergänge verschiedener Strömungsregime bestimmt werden. Da die Strömungskenngrößen ($z.B.\rho ,\overrightarrow{v}$) aufgrund der Numerik diskret sind, helfen folgende Definitionen für Skalarfelder: $$\begin{array}{r}t=k\mathrm{\Delta }t\Rightarrow s(\overrightarrow{x},t)\widehat{=}{s}_i^k\\ {\dot{s}}_i^{k+\frac{n}{2}}\widehat{=}\frac{s_i^{k+n}-s_i^k}{n\mathrm{\Delta }t}\end{array}$$ Außerdem sei $\mathrm{\Delta }{t}_k$ die $k$-te Zeitschrittweite und $\mathrm{\Delta }{V}_i$ das Volumen der $i$-ten Zelle. Im Folgenden wird über Zeitintervalle und Volumina summiert, dafür gilt $T=\sum _k\mathrm{\Delta }{t}_k$ und $V=\sum _i\mathrm{\Delta }{V}_i$.

Methodik zur Bestimmung des Übergangs von L1 in L2

Im Folgenden ist die implementierte Methodik zur Bestimmung des ersten Übergangs von L1 (creeping flow / non-separation regime [0 < RE < 4-5]) zu L2 (closed near-wake regime [4-5 < RE < 30-48]) beschrieben. Der wesentliche Unterschied liegt in der Symmetrie des Flusses bezüglich der y-Achse. Für L1 ist eine hohe Symmetrie zu erwarten, während für L2 aufgrund der sich bildenden Vortices hinter dem Zylinder eine niedrigere Symmetrie zu erwarten ist. Als Maß für die Symmetrie eines Skalarfelds $s$ (z.B. $\rho$) wird folgende Definition verwendet: $$\begin{array}{r}\mathcal{S}(s):=1-{⟨\frac{{⟨{(s(r,{\phi }^{\ast },t)-s(r,\pi -{\phi }^{\ast },t))}^2⟩}_{r,{\phi }^{\ast }}}{{⟨s^2(r,\phi ,t)⟩}_{r,\phi }}⟩}_t=1-\frac{1}{T}\sum _k\frac{\mathrm{\Delta }{t}_k}{\sum _i\mathrm{\Delta }{V}_i(s_i^k{)}^2}\sum _{-\frac{\pi }{2}<\phi <\frac{\pi }{2}}\mathrm{\Delta }V(\phi ){[s^k(\phi )-s^k(\pi -\phi )]}^2\end{array}$$ Hierbei gilt ${\phi }^{\ast }\in (-\pi /2,\pi /2)$ und $\phi \in (0,2\pi )$.

Diese Definition von $\mathcal{S}(s)$ garantiert, dass für Skalarfelder $s(x,y)=-s(-x,y)$ die Symmetrie $\mathcal{S}(s)=-1$ beträgt. Anderesherum gilt für ein Skalarfeld mit $s(x,y)=s(-x,y)$, dass $\mathcal{S}(s)=1$ gilt. Aufgrund der Normierung hat $\mathcal{S}(s)$ immer die Dimension Zahl.

Alternativ kann die Rotation betrachtet werden. Diese sollte aufgrund der Wirbel in L2 größer sein. Als Maß der Rotation eines Vektorfelds $\overrightarrow{f}$ (z.B. $\overrightarrow{v}$) wird folgende Definition verwendet: $$\begin{array}{r}\mathcal{R}(\overrightarrow{f}):=\frac{L}{f_{\mathrm{ext}}}{⟨{(\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{f})}_z⟩}_{r,\phi }\end{array}$$ Hierbei wird der Erwartungswert nur über die obere Hälfte $0<\phi <\pi$ gebildet.

Methodik zur Bestimmung des Übergangs von L2 in L3

Beim Übergang von L2 (closed near-wake regime [4-5 < RE < 30-48]) zu L3 (periodic laminar regime [30-48 < RE < 180-200]) ändert sich das Verhalten des Systems im steady state. In L2 wird nach einiger Zeit ein zeitlich konstanter steady state angenommen, in L3 hingegen verhält sich das System periodisch, d.h. man müsste den Übergang anhand der Zeitableitung der Strömungskenngrößen erkennen können. Dazu wird folgende Größe definiert: $$\begin{array}{r}{\mathcal{C}}_t(s,n):=\frac{{⟨{(\frac{\partial }{\partial t}s(r,\phi ,t))}^2⟩}_{r,\phi ,t}}{{\left(\frac{v_{\mathrm{ext}}}{L}\right)}^2{⟨s^2(r,\phi ,t)⟩}_{r,\phi ,t}}=\frac{\sum _{i,k}\mathrm{\Delta }{t}_k\mathrm{\Delta }{V}_i{({\dot{s}}_i^{k+\frac{n}{2}})}^2}{{\left(\frac{v_{\mathrm{ext}}}{L}\right)}^2\sum _{i,k}\mathrm{\Delta }{t}_k\mathrm{\Delta }{V}_i{(s_i^k)}^2}\end{array}$$ Prinzipiell handelt es sich hier um den Erwartungswert bezüglich Zeit und Ort der Größe ${({\dot{s}}_i^{k+\frac{n}{2}})}^2$. Das $n$ gibt an wie viele Mittelungen bei der Berechnung des diskreten Differenzenquotienten gemacht werden. Aufgrund der Normierung hat ${\mathcal{C}}_t(s,n)$ immer die Dimension Zahl.

Simulationsergebnisse

Ergebnisse für die Symmetrie für verschiedene Reynoldszahlen und Gitter (bei $R_{\mathrm{\infty }}=10$)

Symmetrie der Dichte

Symmetrie $v_x$

Symmetrie $v_y$

Ergebnisse für die Symmetrie für verschiedene Reynoldszahlen und Gitter (bei $R_{\mathrm{\infty }}=100$)

Symmetrie der Dichte

Symmetrie $v_x$

Symmetrie $v_y$

Ergebnisse für die Symmetrie der normierten Geschwindigkeit für verschiedene Reynoldszahlen und Gitter (bei $R_{\mathrm{\infty }}=100$)

Symmetrie der Dichte

Symmetrie $v_x$

Symmetrie $v_y$

Ergebnisse für die Zeitableitung für verschiedene Reynoldszahlen und Gitter (bei $R_{\mathrm{\infty }}=10$)

Zeitableitung der Dichte

Zeitableitung von $v_x$

Ergebnisse für die Zeitableitung für verschiedene Reynoldszahlen und Gitter (bei $R_{\mathrm{\infty }}=100$)

Zeitableitung der Dichte

Zeitableitung von $v_x$

Ergebnisse für die Rotation für verschiedene Reynoldszahlen und Gitter (bei $R_{\mathrm{\infty }}=10$)

Rotation

Rotation der normierten Geschwindigkeit

Ergebnisse für die Rotation für verschiedene Reynoldszahlen und Gitter (bei $R_{\mathrm{\infty }}=100$)

Rotation

Rotation der normierten Geschwindigkeit

Interpretation

Symmetrie $\mathcal{S}$

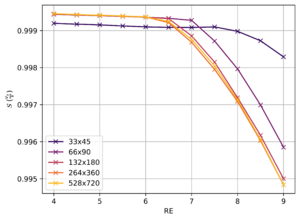
Die Symmetrie $\mathcal{S}$ zeigt für $\overrightarrow{v}$ einen stetigen Übergang von L1 in L2. Daher wurde zusätzlich die Rotation betrachtet. Hierbei ist dasselbe aufgefallen, weshalb die normierte Geschwindigkeit betrachtet wurde. Für die normierte Geschwindigkeiten $v_x/v$ und $v_y/v$ weißt die Symmetrie $\mathcal{S}$ einen Knick bei $\mathrm{Re}\approx 6$ auf.

Rotation $\mathcal{R}$

Die reine Rotation ist beim Übergang von L1 nach L2 auch stetig, allerdings weißt die Rotation des normierten Vektorfelds eine klare Kante auf. Ab einem Bestimmten Punkt entstehen also Wirbel. Um herauszufinden, ob dieser Punkt von der Auflösung des Gitters abhängt, sollten mehrere Gitterauflösungen betrachtet werden. Es wäre durchaus möglich, dass der Sprung nur entsteht, weil die Wirbel erst ab einer Bestimmten Größe (ca. 2 Gitterzellen) vom Gitter aufgelöst werden können. Wie die Abbildungen zeigen, ist dies nicht der Fall, es gibt also eine inhärente minimale Wirbelgröße. Die ersten Wirbel entstehen bei $\mathrm{Re}=6\to \mathrm{Re}=6.5$.

Der Übergang von L1 in L2 scheint also bei etwa $\mathrm{Re}=6$ stattzufinden.

Zeitableitung ${\mathcal{C}}_t$

Für einen kleinen Außenradius ($R_{\mathrm{\infty }}=10$) scheint der Übergang durch $\mathrm{Re}=60$ markiert zu sein, dies ist allerdings scheinbar durch Randeffekte bedingt, da der Übergang für $R_{\mathrm{\infty }}=100$ schon früher stattfindet. Dies wäre auch in besserer Übereinstimmung mit der Literatur, welche einen Übergang bei $30<\mathrm{Re}<48$ angibt. Um hier den Übergangsbereich zu untersuchen, läuft gerade eine Simulation mit mit $R_{\mathrm{\infty }}=100$ für kleinere Reynoldszahlen.