BA Fynn Wawrzyniak/Probleme: Difference between revisions
(+Jet) |
(Schlüsse → Talk-Page) |
||
| Line 166: | Line 166: | ||
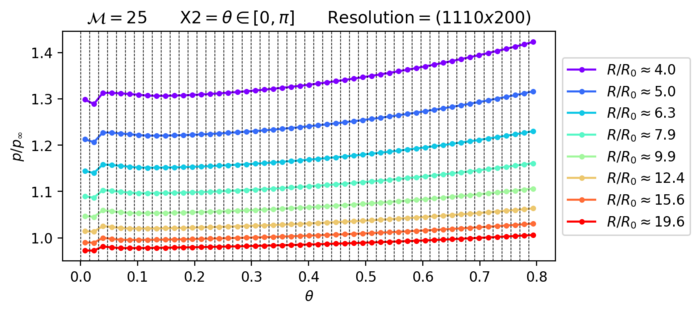
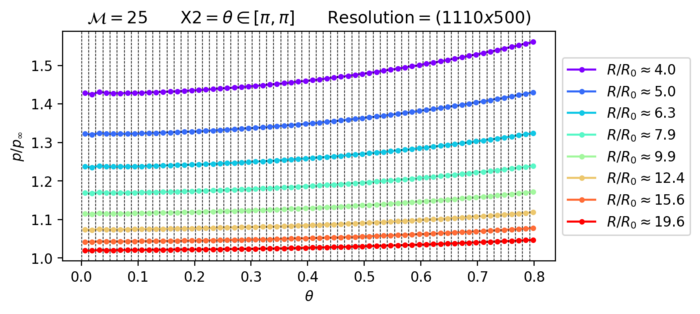
[[File:BA-FW-PROBLEM-JET-M25-FULL-DOMAIN-HIGH-RES-PRS-THETA.png|700px|thumb|center|Fig. 9: Plot des Druckes über Theta, für verschiedene R, für eine Verschiebung der X2-BEG Boundary bei größerer Auflösung]] | [[File:BA-FW-PROBLEM-JET-M25-FULL-DOMAIN-HIGH-RES-PRS-THETA.png|700px|thumb|center|Fig. 9: Plot des Druckes über Theta, für verschiedene R, für eine Verschiebung der X2-BEG Boundary bei größerer Auflösung]] | ||
[[{{TALKPAGENAME}}#Diskussion_zum_"Jet"|Schlüsse aus den Simulationen mit verschiedenen Grid-Setups]] | |||
=== Streamlines für verschiedene Auflösungen === | === Streamlines für verschiedene Auflösungen === | ||
Latest revision as of 15:15, 21 May 2024
negativer Druck
Hilf ein Absenken des initialen Zeitschritts? --Lothar (talk) 07:53, 26 April 2024 (CEST)
Es scheint, dass das Absenken des initialen Zeitschritts nicht hilft. Ich habe einfach mal die logs für verschiedene Einstellung des initialen Zeitschritts beigefügt.
Für \( dt=10^{-10} \)
> Starting computation...
step:0; t = 0.0000e+00; dt = 1.0000e-10; 0.0 %
[Mach = 49.994517]
! ConsToPrim(): p(E) < 0 (-2.34e-05), @step = 66 (stage = 1); [i,j = 2, 73], [x1,x2 = 0.000001, 2.246239]
! ConsToPrim(): p(E) < 0 (-1.27e-05), @step = 66 (stage = 1); [i,j = 2, 74], [x1,x2 = 0.000001, 2.277655]
Für \( dt=10^{-15} \)
> Starting computation...
step:0; t = 0.0000e+00; dt = 1.0000e-15; 0.0 %
[Mach = 49.994517]
step:100; t = 1.3780e-10; dt = 1.3781e-11; 0.0 %
[Mach = 49.995660]
! ConsToPrim(): p(E) < 0 (-3.49e-06), @step = 186 (stage = 2); [i,j = 2, 73], [x1,x2 = 0.000001, 2.246239]
! ConsToPrim(): p(E) < 0 (-1.84e-06), @step = 187 (stage = 1); [i,j = 2, 72], [x1,x2 = 0.000001, 2.214823]
Für \( dt=10^{-20} \)
> Starting computation...
step:0; t = 0.0000e+00; dt = 1.0000e-20; 0.0 %
[Mach = 49.994517]
step:100; t = 1.3780e-15; dt = 1.3781e-16; 0.0 %
[Mach = 49.994517]
step:200; t = 1.8991e-11; dt = 1.8991e-12; 0.0 %
[Mach = 49.994517]
step:300; t = 1.3811e-07; dt = 5.1143e-09; 0.0 %
[Mach = 57.016462]
! ConsToPrim(): p(E) < 0 (-7.80e-06), @step = 307 (stage = 1); [i,j = 2, 73], [x1,x2 = 0.000001, 2.246239]
! ConsToPrim(): p(E) < 0 (-8.17e-06), @step = 307 (stage = 2); [i,j = 2, 73], [x1,x2 = 0.000001, 2.246239]
--Fynn.W (talk) 09:51, 26 April 2024 (CEST)
- Aha, die Schrittweitensteuerung fährt den Zeitschritt wieder rauf (klar), macht ihn dabei aber zu groß. Die Grenze scheint bei \(10^{-11}\) zu liegen. --Lothar (talk) 09:59, 26 April 2024 (CEST)
- Die Ausgabe
[Mach =... ist das Maximum über alle Zellen? --Lothar (talk) 10:28, 26 April 2024 (CEST)
der "Jet"
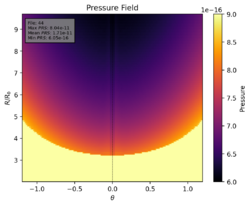
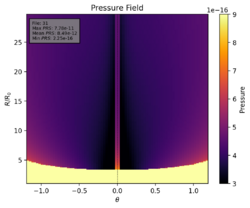
Für größere Mach Zahlen sind in Druck und Dichte Feld ein "Jet" (Shaghayegh) zu erkennen (s. Fig. 1). Der Fehler tritt nur an der X2-Boundary auf, welche in der 'pluto.ini' als 'axisymmetric' definiert wird.
Für das Feld in Fig. 1 wurde auch der minimale Druck aus der 'Restrictions.conf' entfernt, welcher zuvor auf den Wert 1e-16 (in cgs-Einheiten) festgelegt wurde, um die Fehler zu Beginn der Simulation vermeiden zu können. Ich habe diesen Entfernt, weil der unterschied des Minimalen Drucks in der Simulation dem in 'Restrictions.conf sehr ähnlich wurde. Um zu überprüfen ob die Einstellung des minimalen Drucks eine Auswirkung auf den "Jet" hat, habe ich die selbe Simulation mit einem Minimalen Druck von 1e-17 (cgs) druchgeführt. Das Ergebnis ist das selbe. Wenn ich allerdings Versuche den Druck noch kleiner einzustellen treten die Fehler von zuvor wieder auf (ConsToPrim(): p(E) < 0).
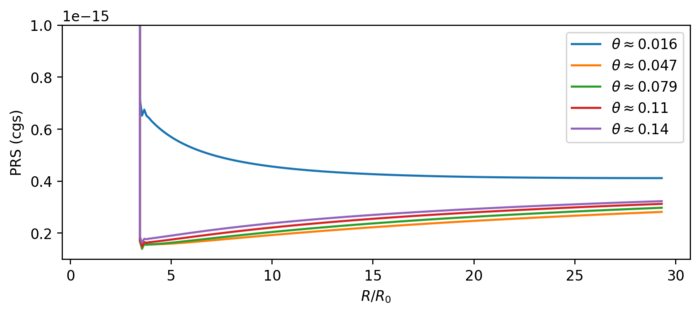
Ich habe auch einmal den Druck in den Zellen für verschiedene Theta geplottet (Fig. 2). Dabei erkennt man, dass die innersten Zellen (\( \theta \approx 0.016 \)) sich vom Verlaufen stark von dass Nachbarn unterscheiden.
Änderung des Gitters
Da in den obigen Simulation der Jet immer nur an den nächsten Zellen zur X2-BEG Boundary zu beobachten war, habe ich für selbe Setup mir verschiedene Gittereinstellungen angeguckt. Geändert habe ich dabei die Position der X2-BEG Boundary und die Auflösung des Gitters. Das Gitter aus den vorherigen Simulation (Auflösung : 550x100) hatte folgende Form:
[Grid]
X1-grid 1 1e-6 550 l+ 20.0
X2-grid 1 0.0 100 u 3.14159265359
X3-grid 1 0.0 1 u 6.28318530718
[Boundary]
X1-beg userdef
X1-end userdef
X2-beg axisymmetric
X2-end axisymmetric
X3-beg periodic
X3-end periodic
Größere Auflösung (1110x200)
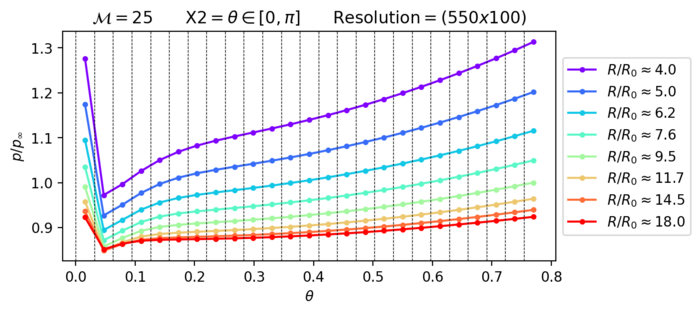
Für den Fall größerer Auflösung ist der "Jet" deutlich kleiner. Dazu dieser nicht mehr an der innersten Zelle der X2-BEG Boundary.
Gitter-Setup in der pluto.ini:
[Grid]
X1-grid 1 1e-6 1110 l+ 20.0
X2-grid 1 0 200 u 3.14159265359
X3-grid 1 0.0 1 u 6.28318530718
[Boundary]
X1-beg userdef
X1-end userdef
X2-beg axisymmetric
X2-end axisymmetric
X3-beg periodic
X3-end periodic
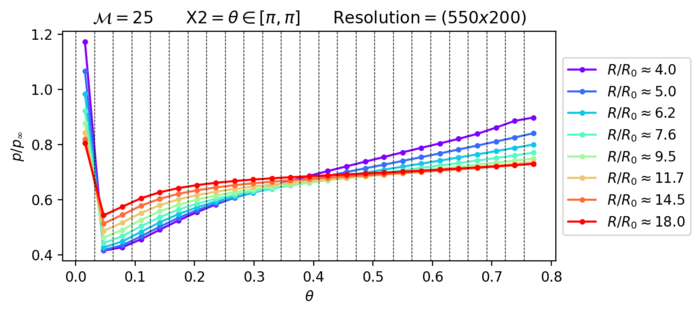
Verschieben der X2-BEG Boundary bei originaler Auflösung (550x200)
Für dieses Grid-Setup entsteht ein sehr ähnlicher Fehler zu dem mit der selben Auflösung aber der originellen X2-BEG Boundary Position.
Gitter-Setup in der pluto.ini:
[Grid]
X1-grid 1 1e-6 550 l+ 20.0
X2-grid 1 -3.14159265359 200 u 3.14159265359
X3-grid 1 0.0 1 u 6.28318530718
[Boundary]
X1-beg userdef
X1-end userdef
X2-beg periodic
X2-end periodic
X3-beg periodic
X3-end periodic
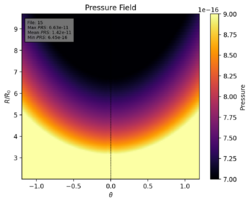
Verschieben der X2-BEG Boundary bei größere Auflösung (1110x500)
Für diesen Fall ist erneut der "Jet" sehr klein und kaum erkennbar.
Gitter-Setup in der pluto.ini:
[Grid]
X1-grid 1 1e-6 1110 l+ 20.0
X2-grid 1 -3.14159265359 500 u 3.14159265359
X3-grid 1 0.0 1 u 6.28318530718
[Boundary]
X1-beg userdef
X1-end userdef
X2-beg periodic
X2-end periodic
X3-beg periodic
X3-end periodic
Schlüsse aus den Simulationen mit verschiedenen Grid-Setups
Streamlines für verschiedene Auflösungen
Mir ist grade auch aufgefallen, dass für verschiedene Auflösungen die Streamlines andres aussehen. Die Streamlines in dem Plot werden auf folgender Line gestartet und in beide Richtungen entwickelt. Dabei sind die Startpunkte auf dieser Line uniform verteilt:
Streamline-Startpunkte:
lineStart: x=0 z=2e-06
lineEnd: x=3e-06 z=2e-06