Evaluator

Der Evaluator ist das Evaluierungswerkzeug, welches von JACK für Berechnungen aller Art (z.B. mathematische und chemische Berechnungen) verwendet wird. Der Evaluator wird daher sowohl für die Erzeugung von Variablen genutzt, als auch um die Prüfregeln für richtige Antworten bzw. Feedbacknachrichten auszuwerten. Er beherrscht eine Reihe von Funktionen, z.B. einfache arithmetische Operationen und Funktionen auf Zeichenketten, ist jedoch auch in der Lage mit Computer Algebra Systemen zu kommunizieren und dort Auswertungen vornehmen zu lassen. Derzeit ist der Evaluator in der Lage mit den beiden externen Systemen Sage und R zu kommunizieren. Der Evaluator bietet neben den oben beschriebenen Basisfunktionen einige CAS-Funktionen an, welche bestimmte festgelegte Auswertungen in den externen Systemen vornehmen. So kann beispielsweise mittels der Funktion isLinearlyIndependent geprüft werden, ob eine Menge von Vektoren linear unabhängig ist. Diese Funktion verwendet intern Sage, um eine Entscheidung zu finden. Der Evaluator meldet das Ergebnis dann an den JACK Kern zurück, welcher dieses weiter verarbeitet. Zudem können mit dem Evaluator auch Funktionen logisch miteinander verknüpft werden, also durch und, oder oder auch nicht.

Verwendung des Evaluators

Verwendung der Evaluator-Ausdrücke im Feedback

Wird in einer Aufgabe beim Feedback eine Evaluator Regel angegeben, dann wird der Ausdruck dem Evaluator übergeben:

Hier wird ein Fill-In Feld darauf geprüft, ob es leer ist.

Der Rückgabewert der verwendeten Funktion muss zwingend ein Wahrheitswert sein. Also entweder es trifft zu und die Funktion gibt True zurück oder es trifft nicht zu und die Funktion gibt False zurück. Es können auch mehrere Funktionen folgendermaßen miteinander verknüpft werden:

Hier werden zwei Fill-In Felder darauf geprüft, ob sie die bestimmten Werte der beiden Variabeln x und y haben.

Logische Operatoren

Die zwei &-Zeichen stehen für die logischen und-Verknüpfung. Es gibt auch die oder-Verknüpfung mit zwei senkrechten Strichen (||) und die nicht-Verknüpfung mit dem Ausrufezeichen (!). Hier ist die Auflistung der Verknüpfung A && B = C, dabei sind A, B Aussagen, die entweder True oder False sind. Daraus ergibt sich dann folgendes für C:

A	B	C
True	True	True
True	False	False
False	True	False
False	False	False

Bei der oder-Verknüfung A || B = C ergibt sich für C folgendes:

A	B	C
True	True	True
True	False	True
False	True	True
False	False	False

Für die nicht-Verknüpfung !A = B ergibt sich für B folgendes:

A	B
True	False
False	True

Variablen erstellen

Hinweis: Siehe auch nähere Informationen zu Variablen.

Der Evaluator kann Variablen, die innerhalb einer Aufgabe definiert wurden, nutzen.

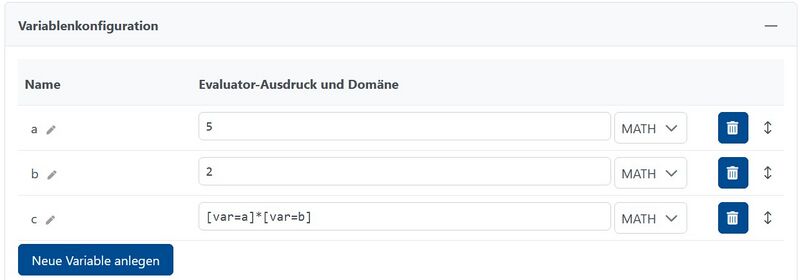
In diesem Beispiel werden die beiden Variablen a und b mit den Werten 5 bzw. 2 erstellt. Außerdem wird eine dritte Variable c erstellt, die das Produkt der beiden vorherigen Variablen bildet. Neben den mathematischen Basisoperationen enthält der Evaluator diverse Funktionen (s.u.), die teilweise auf externe Computer-Algebra-Systeme (Sage, R) zugreifen. Beim Benutzen einer solchen CAS-Funktion kann mittels evaluateInSage() oder evaluateInR() das entsprechende CAS verwendet werden.

In diesem Fall enthält die Variable b die Fakultät der Zahl, die in der Variablen a enthalten ist, berechnet mit Hilfe des CAS Sage.

Funktionen

Die Evaluatoren beinhalten viele verschiedene Funktionen, die alle in JACK für die Aufgabendarstellung benutzt werden können. Unter den hier angegebenen Links finden Sie eine vollständige Liste aller angebotenen Funktionen im entsprechenden Evaluator mit ihrer Funktionalität.

• Math-Evaluatorfunktion
• Chem-Evaluatorfunktion

Welcher Evaluator für einen Ausdruck bzw. eine Variable benutzt wird, entscheidet das Drop-Down rechts neben dem Ausdruck.

Neue Funktionen in JACK3

Für weitere Informationen siehe Evaluator-Änderungen von JACK2 nach JACK3.

Hinweis für JACK2: Wenn man zwei oder mehr Funktionen miteinander verknüpft fallen die Anführungszeichen weg: equalsExpr(evalEq('5','5'),'0').

Ausrechnen von Ausdrücken verhindern

Evaluatorausdrücke werden immer ausgerechnet. Eckige Klammern können eingefügt werden, um das Evaluieren von Gesamt- und Teilausdrücken zu verhindern ("gestoppter Ausdruck"). Ein Beispiel hierfür ist die Definition von Variablen für den Aufgabentext. Hat man bisher x+2*x als Variable angelegt, wurde der Ausdruck zu 3*x zusammengefasst. Fügt man nun [ und ] ein, wird der Ausdruck nicht mehr ausgerechnet.

Ausdruck	Ergebnis (in LaTeX)	Erklärung
x+3*x	\(4 \cdot x\)	Der Ausdruck wird ausgerechnet.
[x+3*x]	\( x+3 \cdot x \)	Der Ausdruck wird nicht ausgerechnet.
getFromList(0,list(x+3*x,[2*x+3*x]))	\( 4 \cdot x \)	Alle Elemente der Liste werden ausgerechnet.
getFromList(1,list(x+3*x,[2*x+3*x]))	\( 2 \cdot x + 3 \cdot x \)	Die Elemente der Liste werden nicht ausgerechnet, sondern sind exakt wie eingegeben.

Die Variablen können allerdings trotzdem zur Bewertung der Aufgabe verwendet werden. Sobald ein "gestoppter" Ausdruck (von [ und ] umschlossen) in einer Funktion verwendet wird, wird diese ausgerechnet. Dies bedeutet, dass ein "gestoppter" Ausdruck nur solange "gestoppt" ist, wie keine Funktion den Wert dieses Ausdrucks verwendet.

Beispiele:

• 3+[x+x] → \(2\cdot x + 3\). Da [x+x] Teil einer Funktion (Summe) ist, wird der Ausdruck ausgerechnet.
• [3+x+x] → \(3+x+x\). Hier ist der Ausdruck selbst eine Summe. Da er hier kein Parameter einer weiteren Funktion ist, wird er nicht ausgerechnet.
• varA := [3+x+x] und varB := [var=varA]+3 → \(2 \cdot x + 6\). Hier ist [3+x+x] wieder Teil einer Summe und wird daher ausgerechnet.
• varA := [3+x+x] und varB := [[var=varA]+3] → \(3+x+x+3\). Hier ist [3+x+x] zwar auch Teil einer Summe; da diese aber auch mit [ und ] umschlossen ist, wird der Ausdruck nicht ausgerechnet.
• getFromList([1+1], list(1,2,3)) → \(3\). Hier ist [1+1] Teil einer Funktion, die den genauen Wert benötigt. Daher wird [1+1] berechnet.

Einige Funktionen, evaluieren die Argumente nicht, um bspw. die Syntax zu analysieren (z.B. isIntegerNumber, isMatrix, isSum, isProduct, ...).

Weitere Beispiele und Vergleiche

Variablenname	Ausdruck	Wert
[var=A]	1+1	2
[var=B]	[1+1]	1+1
[var=C]	1+[var=A]	3
[var=D]	1+[var=B]	3
[var=E]	[1+[var=A]]	1+2
[var=F]	[1+[var=B]]	1+1+1
[var=J]	getFromList(1,list(2,3,4))	3
[var=K]	getFromList(1,list(2,[2+5],4))	2+5
[var=L]	getFromList(1,list(2,[var=A],4))	2
[var=M]	getFromList(1,list(2,[[var=B]],4))	1+1 (zu beachten ist hier, dass zum "Stoppen" von B doppelte Klammern erforderlich sind)
[var=N]	getFromList([1+1],list(2,3,4))	4
[var=O]	getFromList([var=A],list(2,3,4))	4
[var=P]	getFromList([var=B],list(2,3,4))	4
[var=P2]	getFromList([[var=B]],list(2,3,4))	4, B wird hier zwangsläufig ausgerechnet.
[var=Q]	[getFromList(1,list(2,3,4))]	3 (die Listenfunktion selbst kann nicht gestoppt werden)
[var=Q2]	[getFromList(1, list(1+1,2+2,3+3))]	2+2 (die einzelnen Elemente werden nicht ausgerechnet)
[var=R]	[random()]	Beispiel: 0.547 (random() selbst kann nicht gestoppt werden)
[var=R2]	[random()+random()]	Beispiel: 0.871+0.219 (die Addition wird beibehalten)
[var=S]	[getRandomFromList(list(1,2,3,4,5))]	Beispiel: 3
[var=S2]	[getRandomFromList(list(1+1,2+2,3+3))]	Beispiel: 1+1 (die einzelnen Elemente werden nicht ausgerechnet)
[var=T]	isIntegerNumber([1+1])	false
[var=U]	isIntegerNumber(1+1)	false
[var=V]	isIntegerNumber([var=A])	true
[var=W]	isIntegerNumber([var=B])	false
	sqrt(9)	3
	[sqrt(9)]	\( \sqrt(9) \)
	sqrt(1 + 3)	2
	[sqrt(1 + 3)]	\( \sqrt(1+3) \)
	sqrt([1 + 3])	2, da der Ausdruck in eckigen Klammern innerhalb einer Funktion auftaucht