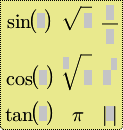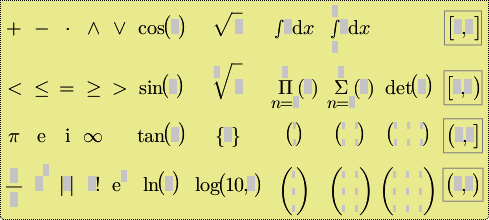Standardpaletten: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Spobel (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
PRanz (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 98: | Zeile 98: | ||
* [[Formeleditor]] | * [[Formeleditor]] | ||
* [[Templatepaletten]] | * [[Templatepaletten]] | ||
[[category:Formeleditor]] | |||
Version vom 5. Dezember 2018, 12:02 Uhr
Beschreibung
Eine Standardpalette ist eine systemweit verfügbare Palette, die im Formeleditor in JACK eingesetzt werden kann.
Übersicht
| Basic |
|
Diese Palette wird für einen Großteil der Aufgaben verwendet. Es besitzt nur grundlegende mathematische Formeln. Diese wären:
|
| Trigonometrie |
|
Dieser Formeleditor enthält neben den Formeln des Basic-Editors außerdem Sinus, Kosinus, Tangens und das Symbol für Pi. Somit ist diese Palette besonders gut für Trigonomieaufgaben geeignet. |
| Palette |
|
Die Palette erweitert den Trigonometrie-Editor (und damit auch den Basic-Editor) erneut um eine breit gefächerte Auswahl von Symbolen. Sie enthält unter anderem
|
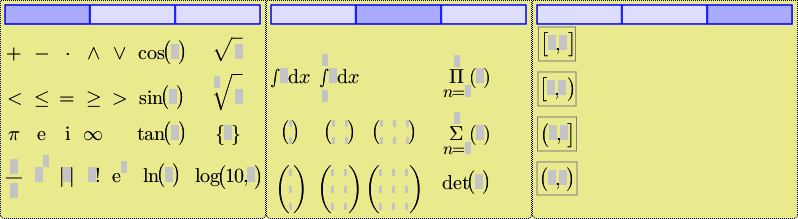
| Palette Full |
|
Die Palette Full enhält die meisten Einträge, die auch in der regulären Palette enthalten sind. Zusätzlich verfügt sie über eine zweite Seite, auf der diverse weitere Funktionen zu finden sind. |
| Palette Split |
|
Die aufgeteilte Palette enthält alle Einträge der Palette, allerdings auf drei Seiten verteilt, so dass der Editor kompakter wird. |
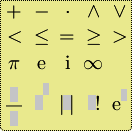
| Palette2 |
|
Diese Palette grundlegende mathematische Operatoren, Vergleichsoperationen, gängige mathematische Konstanten. |
| Palette3 |
|
Palette3 entspricht größtenteils der Palette, jedoch ohne Intervalle dafür mit dem Verkettungssymbol. |
| Palette4 |
|
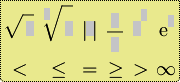
Die vierte Palette besteht aus der siebten Wurzel, Beträgen, Brüchen, Potenzen und der e-Funktion. |
| Palette5 |
|
Die Palette5 enthält das Gleiche wie die Palette4 erweitert um beliebige Wurzeln, Vergleichsoperationen und das Unendlichsymbol. |
| Palette6 |
|
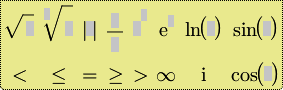
Die Palette6 erweitert die Palette5 um die Sinus- und Kosinusfunktionen, sowie den natürlichen Logarithmus und die imaginäre Einheit i der komplexen Zahl. |