Talk:BA Emilio Schmidt

Hier auf der Talk-Seite können wir Diskussionen führen und dabei natürlich auch Links verwenden. Hochgradig sinnvoll ist es, seine Beiträge zu signieren, was einfach durch das Anhängen von ~~~~ geschieht (oder auch im Edit-Feld oben der Knopf zwischen dem I-Knopf und dem Link-Knopf). Zur Strukturierung von Threads kann man noch mit Doppelpunkten einrücken. --Lothar (talk) 10:23, 16 April 2024 (CEST)

Ableitungen des v-Feldes an der Kugeloberfläche

Möchte man die Scherung im Gas wissen oder die Scherung zwischen dem Gas und der Null-Geschwindigkeit an der Kugeloberfläche? --Rolf

Ich sehe da analytisch keinen Unterschied. Das v-Feld ist bis an die Kugel heran definiert, dort sind eigentlich die Ableitungen auszuwerten. Wenn wir im Post-Processing die Werte in den Geisterzellen nicht haben, müssen wir passende, d.h. extrapolierende Diskretisierungsformeln verwenden. --Lothar (talk) 10:48, 16 April 2024 (CEST)

Ich meine damit sowas wie $(f(3h/2)-f(h/2))/h=f^{\prime }(0)+\mathcal{O}(h)$ oder $(-f(5h/2)+3f(3h/2)-2f(h/2))/h=f^{\prime }(0)+\mathcal{O}(h^2)$. --Lothar (talk) 11:57, 16 April 2024 (CEST)

Du hattest gestern gesagt, dass es zu Problemen mit der Funktion np.gradient() kommen könnte, wegen der nicht äquidistanten Zellen. Ich habe nochmal auf der Webseite von numpy nachgeschaut (numpy.gradient). Dort steht, dass die Funktion auch für nicht äqudistante Schrittweiten verwendbar ist, solange die Liste angegeben wird, nach der abgeleitet werden soll. Aufgrund dessen, dass beide Geschwindigkeitskomponenten auf der Kugel gleich Null werden müssen, können wir diese manuell in die Geschwindigkeitsfelder hinzufügen. Dann müsste man nur noch schauen, wie man den fehlenden Teil bei $\theta =0$ extrapoliert. --Emilio.S (talk) 10:10, 23 April 2024 (CEST)

Ja, verstehe np.gradient() bietet den Vorteil, dass Du mit einem Aufruf die $r$-Ableitung für alle $\theta$ (außer 0) berechnen lassen kannst. Bei der Ableitung nach $\theta$ haben wir eh noch das "Problem", dass wir zwar alle $\theta$-Werte (außer 0) haben, aber auswerten wollen wir ja auch die bei $r=R$. Erst aber sollten wir die Ordnung festlegen. Ich schlage vor, sich zunächst auf die 1. Ordnung zu beschränken. --Lothar (talk) 13:01, 23 April 2024 (CEST)

Meinst du mit "Problem", dass alle $u_{\theta }$ bzw. $u_r$ für $r=R$ gleich Null sind? Würden sich dann nicht die Ableitungsterme nach $\theta$ einfach wegfallen? Falls dies nicht der Fall ist soll ich die Ableitungen nach $\theta$ nicht mit np.gradient() bestimmen, da diese Funktion einen Fehler 2. Ordnung hat (s.numpy.gradient).--Emilio.S (talk) 16:50, 23 April 2024 (CEST)

Äh, ja, stimmt, die Ableitungen nach $\theta$ fallen in der Tat bei $r=R$ weg, da $u_r$ und $u_{\theta }$ dort konstant Null sind. Super, das macht $\underset{―}{\underset{―}{\sigma }}$ noch einfacher. --Lothar (talk) 18:13, 23 April 2024 (CEST)

Ja da würden jetzt überraschend viele Terme wegfallen, am Ende würden meiner Meinung nach neben dem Druck-Term nur noch zwei weitere Terme übrig bleiben. Ich änder das heute oder morgen mal in dem Wiki dann kannst du ja mal drüber schauen.--Emilio.S (talk) 19:00, 23 April 2024 (CEST)

Habe ich. --Lothar (talk) 18:52, 24 April 2024 (CEST)

---

Dann noch mal zu $r=R,\theta =0$: Dort gilt ja $u_r=u_{\theta }=0$ (no slip) und Selbiges für die 1. Ableitung nach $\theta$ (Symmetrie). Sei nun $\mathrm{\Delta }{r}_0=h$ und $\mathrm{\Delta }{r}_1=qh$, dann kommt bei mir raus: $$\frac{\partial u}{\partial r}{|}_{r=R,\theta =0}=\frac{3(q+2)(3q+5)u_{00}-(q^2+q-2)u_{01}+3(q-1)u_{10}-(3q+5)u_{11}}{4h(q+1)(q+2)}+\text{Terme 2. Ordnung}$$ Dabei zählt in $u_{ij}$ der Index $i$ die $r$-Zellen und $j$ die $\theta$-Zellen, also $u_{00}=u(r=\mathrm{\Delta }{r}_0/2,\theta =\mathrm{\Delta }\theta /2)$ usw. Mich erstaunt noch etwas, dass $\mathrm{\Delta }\theta$ rausfällt, das liegt wohl an der verschwindenden 1. Ableitung. Aber jetzt, wo ich fertig bin: Zum Integrieren gemäß der Mittelpunktregel brauchen wir den Wert doch gar nicht. --Lothar (talk) 18:52, 24 April 2024 (CEST)

Genau der Wert für $\theta =0$ und für $\theta =\pi$ fällt zusätzlich auch wegen dem Flächenelement weg, da der $\sin (\theta =0)=\sin (\theta =\pi )=0$ ist.--Emilio.S (talk) 11:31, 26 April 2024 (CEST)

Falls doch noch mal jemand sowas braucht, für den äquidistanten Fall $q=1$ vereinfacht es sich zu $$\frac{\partial u}{\partial r}{|}_{r=R,\theta =0}=\frac{9u_{00}-u_{11}}{3h}+\text{Terme 2. Ordnung}.$$ --Lothar (talk) 10:10, 25 April 2024 (CEST)

Dimensionslose Kenngröße

Von den 4 das Szenario beschreibenden Parametern, $v,R,\rho$ und $\mu$, lässt sich aus keinem Trio eine dimensionslose Größe bilden (lässt sich abbilden auf 4 Vektoren $\in {\mathbb{Z}}^3$, von denen keine 3 komplanar sind). Alle möglichen dimensionslosen Kombinationen der 4 unterscheiden sich daher von der Standardkombination Reynoldszahl höchstens dadurch, dass sie Potenzen von ihr sind. Damit wissen wir, dass für die Kraft auf die Kugel $$F=F_{0}f(\text{Re})$$ gelten muss, wobei $F_0$ eine aus 3 der Parameter gebildete Kraft-Einheit ist. Da wir schon wissen, dass $F$ zumindest im Stokes-Regime die Viskosität enthält, bilden wir $F_0$ aus den anderen 3 (Trägheit): $$F_0=\rho v^2{R}^2$$ und erhalten so fürs Stokes-Regime $$\frac{F}{F_0}=6\pi \frac{2}{\text{Re}}$$ d.h. $f(x\to 0)\to 12\pi /x$. (Auch bekannt: $f(x\to \mathrm{\infty })\to \text{const.}$)

Die Wahl von $F_0$ legt außerdem nahe, die 3 Größen $\rho ,v$ und $R$ fest zu lassen (Zahlenwerte 1 im Code) und die Reynoldszahl über $\mu$ zu variieren. In der natürlichen Einheit $\rho vR$ hat $\mu$ den Zahlenwert $2/\text{Re}$. --Lothar (talk) 08:31, 17 April 2024 (CEST)

Eine alternative Krafteinheit wäre $F_1={\mu }^2/\rho ={\nu }^2\rho$, damit gilt im Stokes-Regime $$\frac{F}{F_1}=3\pi \text{Re}$$ und man würde $\rho ,R$ und $\mu$ bzw.\ $\nu$ fest lassen (Zahlenwerte 1 im Code) und die Reynoldszahl über $v$ variieren. In der natürlichen Einheit $\mu /(\rho R)=\nu /R$ hat $v$ den Zahlenwert $\text{Re}/2$. --Lothar (talk) 09:29, 17 April 2024 (CEST)

Auch wenn die Krafteinheit $F_1$ nicht so anschaulich ist, ist der "Durchstimm"-Zusammenhang $v=\text{Re}/2$ IMHO vorzuziehen. --Lothar (talk) 17:49, 18 April 2024 (CEST)

Ich wollte nochmals sicher gehen, ob ich das ganze mit den natürlichen Einheiten verstanden habe. Wir wählen also aus irgendeinem Grund bestimmte charakteristische Größen des Systems aus, welche dann gleich $1$ gesetzt werden und drücken dann weitere Größen in Bezug zu diesen natürlichen Einheiten aus? Im Moment sind bei mir in der Datei user-defined.parameters.h die Dichte, Länge und die Geschwindigkeit gleich $1$ gewählt. Damit lassen sich es, wie du es schon getan hast die, die Masse, Länge und Zeit in diesen natürlichen Einheiten ausdrücken. Die dynamische Viskosität $\mu$ lässt sich damit nun auch in natürlichen Einheiten ausdrücken. Aufgrund dessen, dass die dynamische Viskosität eine Dimension von $\frac{M}{LT}$ hat, lässt sich die dynamische Viskositätseinheit folgendermaßen schreiben:

$$\begin{array}{r}\rho vR\end{array}$$

Damit folgt für die dynamische Viskosität $\mu =\frac{\rho vR}{Re}$ in den natürlichen Einheiten:

$$\begin{array}{r}\frac{\mu }{\rho vR}=\frac{1}{Re}(\ast )\end{array}$$

Du hattest da jedoch noch einen Faktor $2$ zusätzlich gehabt. Liegt das an der Konvention, dass $L=2R$ gewählt wird?

Analoges Vorgehen liefert dann für die Kraft in natürlichen Einheiten:

$$\begin{array}{r}\frac{F}{\rho v^2{R}^2}=6\pi \frac{2}{Re}\end{array}$$

Soll ich dann diese Formel für die Kraft in mein Notebook implementieren?--Emilio.S (talk) 12:01, 29 April 2024 (CEST)

● "aus irgendeinem Grund": Der Grund ist (u.A.) die Reduktion der Dimension des Parameterraums um 3.

● "gleich $1$ gesetzt werden": Ihr Zahlenwert in den aus ihnen gebildeten Einheiten wird automatisch 1.

● "lässt sich die dynamische Viskositätseinheit folgendermaßen schreiben": Richtig ist $\mu =(\mathsf{\text{Zahlenwert von }}\mu )\cdot \rho vR$. Im "Theoretiker-Alltag" ignoriert man meist den "Operator" $\mathsf{\text{Zahlenwert von}}$ und benutzt dasselbe Symbol für physikalische Größe und ihren Zahlenwert. Erst aus dieser "Schludrigkeit" resultiert dann ein Statement wie $\rho =v=R=1$.

● Deine Gleichung $(\ast )$ gilt (modulo dem Faktor 2) in allen Einheitensystemen (auch z.B. SI oder cgs), die Form ist zur Verdeutlichung gewählt, da die gewählte natürliche Einheit explizit im Nenner steht. Im Code würde die Gleichung dann $\mu =1/\text{Re}$ bzw. $\mu =2/\text{Re}$ lauten. Und ja, der Faktor 2 kommt von $L=2R$.

● "Analoges Vorgehen liefert dann für die Kraft in natürlichen Einheiten": Genauer gesagt, der Zahlenwert der Kraft in diesen Einheiten, den Du aus Deinen Simulationsdaten herausbekämest, sollte ungefähr gleich $12\pi /\text{Re}$ sein.

● "Soll ich dann diese Formel für die Kraft in mein Notebook implementieren?": Das geht nicht, die Kraft ist das Ergebnis. Als Einheitensystem favorisiere ich jedoch die "zähen Einheiten". --Lothar (talk) 08:16, 30 April 2024 (CEST)

Ich glaube ich habe mich da falsch ausgedrückt. Ich meine, ob ich dann die Kraft, welche wir dann mit der Formel

$$\begin{array}{r}F=3\pi Re,\end{array}$$

als Referenzwert nehmen und nicht

$$\begin{array}{r}F=6\pi \mu Rv.\end{array}$$

So ist es, genau. --Lothar (talk) 22:39, 6 May 2024 (CEST)

Ich habe heute noch ein paar Simulationen laufen lassen, bei feiner gewählten Zellen und die aus den Daten bestimmte Kraft dann mit $F=3\pi Re$ verglichen. Die Abweichung wird dabei immer kleiner für sehr fein gewählte Zellen. --Emilio.S (talk) 21:33, 1 May 2024 (CEST)

Kraftberechnung (Emilio)

$$ Kleiner Einwand: Aus der $\phi$-Unabhängigkeit der entsprechenden $\underset{―}{\underset{―}{\sigma }}$-Komponenten folgt natürlich nicht ihr Verschwinden. --Lothar (talk) 17:49, 18 April 2024 (CEST)

Ich bin nicht d'accord mit Deiner Begründung hinsichtlich der z-Richtung. Klären wir aber vielleicht am besten IRL. --Lothar (talk) 18:35, 18 April 2024 (CEST)

Alles klar, können wir machen --Emilio

Ein Statement schon mal vorab: Von einer Kraftkomponente in $r$-, $\theta$- bzw. $\phi$-Richtung zu sprechen ergibt generell nur Sinn bei einem Kraftfeld. Unser $\overrightarrow{F}$ ist keines. (Signieren kannst Du übrigens einfach mittels ~~~~, auch per Button.) --Lothar (talk) 06:08, 19 April 2024 (CEST)

Mir ist noch ein etwas größerer Fehler bei meiner vorherigen Rechnung heute morgen aufgefallen, nachdem du weg warst. Ich habe nämlich auch den Divergenzterm in der $\theta r$-Komponente mitgeschleppt, obwohl dieser im Tensor nur auf der Hauptdiagonalen steht, da der Divergenzterm mit dem Einheitstensor multipliziert wird. Dadurch wird die Endgleichung ein wenig schlanker. --Emilio.S (talk) 15:18, 19 April 2024 (CEST)

Implementierung in Python

Ich habe jetzt auf der Wiki-Seite grob erklärt, wie ich bis jetzt die Kraftberechnung in Python implementiert habe. Ich kann Dir auch noch mein Notebook per Mail schicken. Ich werde mich jetzt mit dem Problem befassen, dass meine Kraft nach oben zeigt und nicht wie erwartet nach unten.--Emilio.S (talk) 11:27, 26 April 2024 (CEST)

Ich glaube das Problem liegt an der radialen Ableitung. Ich bin der Meinung, dass die Ableitung entlang der Stromlinie ausgerechnet werden muss. Da wir jedoch in Kugelkoordinaten rechnen, berechnen wir ja oberhalb der Kugel die radiale Ableitung aus Sicht der Kugel aus, was zu einem Vorzeichenfehler meiner Meinung nach führt.--Emilio.S (talk) 13:28, 26 April 2024 (CEST)

Ich habe die Funktion für die Ableitung entsprechend angepasst und auf der Wiki-Seite hochgeladen.--Emilio.S (talk) 15:16, 26 April 2024 (CEST)

---

Ich glaube ich habe den Fehler gefunden, der dafür sorgt, dass die Kraft für ein feineres Grid immer größer wird. Es liegt glaube ich daran, dass ich das $d\theta$ bei der Integration bzw. dann Summation der $d\overrightarrow{F}$ vergessen habe mitzunehmen. --Emilio.S (talk) 16:10, 3 May 2024 (CEST)

Ich habe das jetzt auf der Main Paige geändert und erneut die Kräfte für die verschieden feinen Grids bestimmt. Dabei habe ich immer ganzzahlige Vielfache in der Zellaufteilung im Vergleich zu meinem Ausgangsgrid genommen. Es scheint hierbei so, als ob die Werte für immer feinere Grids gegen einen bestimmten Wert konvergieren. Um dies bestätigen zu können muss ich jedoch mehr Simulationen laufen lassen. Es fällt jedoch auf, dass die numerisch bestimmten Werte dann um einen Faktor 20 ungefaähr vom theoretisch erwarteten Wert abweichen.--Emilio.S (talk) 16:53, 3 May 2024 (CEST)

Fehler in der numerischen Kraftberechnung

Es stellt sich heraus, dass die relative Kraftabweichung, selbst für vergleichsweise hohe Auflösungen, trotz der Auflösung im Bereich von ungefähr $20\mathrm{\%}$ liegt. Dies lässt sich auch anhand Abb.1 erkennen.

Abb.1: Relative Kraftabweichung von der theoretisch erwarteten Kraft aufgetragen über das Verhältnis der Auflösung bzgl. des Ausgangsgrids

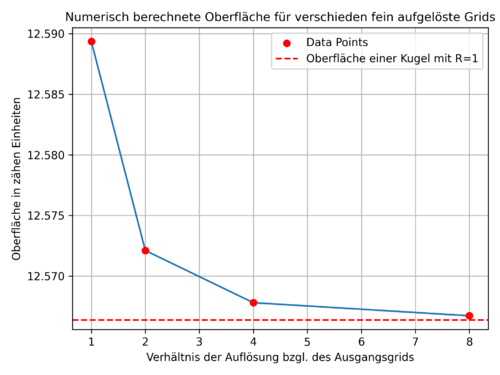
Dieser Fehler könnte jedoch viele Ursachen haben. Eine davon könnte die numerisch durchgeführte Integration sein, welche einer einfachen Summation entspricht. Um dies zu überprüfen, wird zunächst das Oberflächenintegral über die Kugel bestimmt. Dabei wird analytisch für eine Kugel mit Radius $R=1$ eine Kugeloberfläche von $A=4\pi$ erwartet. In Abb.2 sind die numerisch berechneten Oberflächenintegrale für die jeweiligen Grids aufgetragen und es lässt sich erkennen, dass der analytische Wert für eine Auflösung vom Faktor 8 schon sehr gut genähert wird. Daher lässt sich vermuten, dass die numerische Integration nicht der Grund für den Fehler in der Kraftberechnung ist.

Abb.2: Numerisch berechnetes Oberflächenintegral aufgetragen über die jeweilige Auflösung des Grids

Daher muss der Fehler entweder durch die Druckverteilung oder das Geschwindigkeitsfeld kommen. Um dies zu untersuchen wird zunächst die Druckverteilung für die ersten beiden Zellschalen um die Kugel untersucht. In In Abb.3 lässt sich erkennen, dass die analytischen Lösungen bzw. die numerischen Lösungen für die ersten beiden Zellschalen nahezu perfekt übereinander liegen. Auch weisen die numerischen Lösungen einen kosinusförmigen Verlauf auf, genau, wie analytisch erwartet. Jedoch ist die numerische Lösung für $\theta <\frac{\pi }{2}$ stets größer bzw. für $\theta >\frac{\pi }{2}$ stets kleiner als die analytische Lösung. Die Peaks der numerischen Lösungen weichen hierbei um ungefähr $20\mathrm{\%}$ von der jeweiligen analytischen Lösung ab.

Abb.3: Druckverlauf der ersten beiden Zellschalen, für eine Reynoldszahl von $Re=\frac{1}{100}$ und einer Auflösung vom Faktor $8$, aufgetragen über den Winkel $\theta$

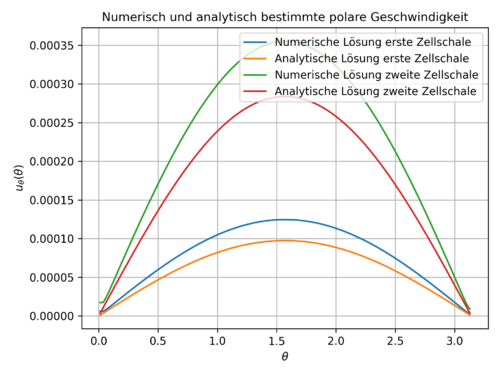
Analog lässt sich die polare Geschwindigkeit $u_{\theta }$ für die ersten beiden Zellschalen um die Kugel untersuchen. In Abb.4 lässt sich dann erkennen, dass die analytischen Lösungen und numerischen Lösungen für die jeweiligen Zellschalen, qualitativ ähnlich verlaufen. Jedoch weichen die Peaks der numerischen Lösungen für beide Zellschalen um ungefähr $20\mathrm{\%}$ voneinander ab.

Abb.4: Polare Geschwindigkeit $u_{\theta }$ der ersten beiden Zellschalen, für eine Reynoldszahl von $Re=\frac{1}{100}$ und einer Auflösung vom Faktor $8$, aufgetragen über den Winkel $\theta$

In Abb.5 ist selbige Untersuchung, wie in Abb.4, für die radiale Geschwindigkeitskomponente $u_r$ angestellt worden. Hier fällt auf, dass die jeweiligen numerischen und analytischen Kurven, erneut qualitativ ähnlich verlaufen, außer für die Winkel $\theta =0$ und $\theta =\pi$. Außerdem fällt auf, dass die Abweichung der Peaks deutlich größer ist, als in Abb.3 und Abb.4. Für die erste Zellschale weicht die numerische Lösung ungefähr um einen Faktor $2$ und für die zweite Zellschale um einen Faktor $1,5$ ab.

Abb.5: Radiale Geschwindigkeit $u_r$ der ersten beiden Zellschalen, für eine Reynoldszahl von $Re=\frac{1}{100}$ und einer Auflösung vom Faktor $8$, aufgetragen über den Winkel $\theta$

Ich finde, der Abschnitt mit den Plots könnten eigentlich auf die Hauptseite. Aktuelle Fragen:

• Bleiben bei Halbierung der Reynoldszahl die relativen Abweichungen gleich?
• Wie wirkt sich ein größerer Außenradius aus? --Lothar (talk) 17:43, 16 May 2024 (CEST)

Viskosität, dynamisch vs. kinematisch

Von den beiden, $\mu =\nu \rho$, ist keine ein wirklicher Materialparameter, doch die dynamische Viskosität hängt nur von der Temperatur (und von WW-Details der Fluid-Partikel) ab. Da im Stokes-Regime die Temperatur-Änderung klein sein sollte, ist es also sinnvoller, $\mu$ als "Materialparameter" vorzugeben.

Die Viskosität wird in der Funktion Visc_nu() in visc_nu.c berechnet, ein Aufruf pro Zelle. Trotz der Namen nu1 (Scherv.) und nu2 (Volumenv.) handelt es sich um die dynamischen Viskositäten. Beim Vorgeben von $\mu$ sollte $\rho$ (im Code v[RHO]) also gar nicht auftauchen. Verwendet man obige "zähe Einheiten", so wird die Funktion besonders einfach:

void Visc_nu(double *v, double x1, double x2, double x3, double *nu1, double *nu2)
/* ... */
{
  *nu1 = 1.0;  *nu2 = 0.0;
}