Windtunnel/Boundary Conditions

up

New Keywords

in pluto.ini

• ObjectType_int: 0=nothing, 1=cylinder/sphere, 2=square/cube of size ObjectDiameter_cm
• WindPressure_Pa, WindPressure_mbar (mutually exclusive): pressure at entry (left)
• PressureGradient_mbar_per_cm positive (even though pressure drops from left to right)
• Wind velocity is ramped up to WindVelocity_m_per_s over time InjectionTime_s
• WindTemperature_C
• KinematicViscosity_m2_per_s, DynamicViscosity_Pa_s,
• Wall_BoundaryCondition for tangential walls, value from {0,1,2,3}

(ignored if given values <0)

in init.c

• macro SOLID to enable an object
• array solid containing value 1 or 0 for object matter being present/absent

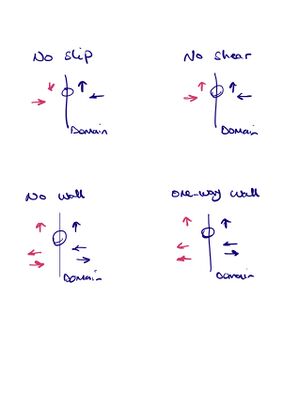
Walls

tangential

Boundary condition for the wall
	vx1	vx2
no-shear	zero-gradient	reflective
no-slip	reflective	reflective
no-wall	zero-gradient	zero-gradient
one-way wall	zero-gradient	zero-gradient & no-inflow

entry/exit

prescribe pressure drop (left to right)

• current simulation result: \(v_x\)-profile slightly asymmetric and \(v_x<0\) at one wall

Open Questions

Reflective cells

Setting the vector \(\vec v_g\) in a ghost cell as \(\vec v_g=-\vec v\), with \(\vec v\) being the value in the adjacent real cell, yields \(\vec 0\) as interpolation right at the boundary. This works for plane walls. What to do in cases where a ghost cell has more than one real cell as nearest neighbor? This calls for discussion!

Analytical Solutions

empty circular tube

$$ v(r) = \frac{\text dp}{\text dx}\frac{R^2-r^2}{4\mu} $$

with \(\mu\)=dynamical viscosity