BA Emilio Schmidt

↑ up ↑

Grundlagen

Gesucht ist ein Zusammenhang für die Kraft $\overrightarrow{F}$, die auf eine von einem viskosen Fluid mit der Einstromgeschwindigkeit $\overrightarrow{v}=-v{\overrightarrow{e}}_z$ umströmte Kugel mit dem Radius $R$ wirkt.

Dabei werden hier in sehr guter Näherung laminare Strömungen betrachtet. Eine Größe, die die Laminarität bzw. Turbulenz einer Strömung charakterisiert ist die Reynolds-Zahl $\text{Re}$. Sie ist eine dimensionslose Größe, welche definiert ist durch: $$\begin{array}{r}\text{Re}=\frac{\rho vL}{\mu }\end{array}$$

Hierbei ist $\rho$ die Dichte des Fluids, $v$ die Geschwindigkeit des Fluids, mit der es auf das angeströmte Objekt zufließt, $L$ die charakteristische Länge des angeströmten Körpers und $\mu$ die dynamische Viskosität des Fluids. Strömungen, welche sich weit im laminaren Regime befinden, werden dann durch $\text{Re}\ll 1$ beschrieben.

Analytische Herleitung der Stokes'schen Formel

Die auf die Kugel wirkende Kraft lässt sich in zwei separate Beiträge unterteilen. Einerseits kann eine Kraft aufgrund eines Druckgradienten um die Kugel wirken, andererseits kann eine Kraft infolge von Scherungseffekten an der Kugeloberfläche auftreten.

Die Kraft auf die Kugel lässt sich dann über den Spannungstensor $\underset{―}{\underset{―}{\sigma }}$ berechnen: $$\begin{array}{r}\overrightarrow{F}={\oint }_{\partial V}\underset{―}{\underset{―}{\sigma }}\cdot \text{d}\overrightarrow{A}\end{array}$$

Der Spannungstensor beschreibt dabei die Verteilung von Kräften bzw. Spannungen in einem Material. Er gibt an jedem Punkt eines Kontinuums die internen Kräfte bzw. Spannungen an, die aufgrund von äußeren Krafteinwirkungen wirken. Der Spannungstensor ist ein Tensor 2. Stufe, dessen Komponenten ${\sigma }_{ij}$ die Spannungen, die aufgrund von Kräften in Richtung der $j$-ten Koordinatenachse auf eine Fläche mit einer Normalen in Richtung $i$-ten Koordinatenachse wirken, repräsentieren. Im Allgemeinen ist der Spannungstensor gegeben durch: $$\begin{array}{r}\underset{―}{\underset{―}{\sigma }}=-[p-\zeta (\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u})]\mathbb{1}+\mu [\overrightarrow{\mathrm{\nabla }}\overrightarrow{u}+(\overrightarrow{\mathrm{\nabla }}\overrightarrow{u}{)}^T-\frac{2}{3}(\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u})\mathbb{1}]\end{array}$$

Dabei ist $p$ das Druckfeld, $\zeta$ die Volumenviskosität, $\overrightarrow{u}$ das Geschwindigkeitsfeld und $\mathbb{1}$ der Einheitstensor. Um den Spannungstensor bestimmen zu können, müssen also zunächst das Geschwindigkeitsfeld $\overrightarrow{u}$ und das Druckfeld $p$ bestimmt werden. Dafür müssen die Kontinuitätsgleichung und die Navier-Stokes-Gleichung gelöst werden, welche im Allgemeinen gegeben sind durch: $$\begin{array}{rl}& \frac{\partial \rho }{\partial t}+\overrightarrow{\mathrm{\nabla }}\cdot (\rho \overrightarrow{u})=0\\ & \rho (\frac{\partial \overrightarrow{u}}{\partial t}+(\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u})=-\overrightarrow{\mathrm{\nabla }}p+\mu \mathrm{\Delta }\overrightarrow{u}+\frac{\mu }{3}\overrightarrow{\mathrm{\nabla }}(\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u})+{\overrightarrow{f}}_{\text{ext}}\end{array}$$

Dabei ist ${\overrightarrow{f}}_{\text{ext}}$ eine externe Kraftdichte. Diese Gleichungen sind jedoch im Allgemeinen nicht analytisch zu lösen, weshalb zusätzliche Annahmen über das System zu treffen sind. Dabei wird hier davon ausgegangen, dass es sich bei vorliegendem Fluid um ein Newtonsches Fluid handelt, woraus folgt, dass die dynamische Viskosität $\mu =\text{const.}$ ist. Zusätzlich folgt dann nach der Stokes'schen Hypothese, dass die Volumenviskosität für Newtonsche Fluide vernachlässigt werden kann: $$\begin{array}{r}\zeta =0\end{array}$$

Außerdem lässt sich, aufgrund der in sehr guter Näherung laminaren Strömung annehmen, dass das Fluid inkompressibel ist, da die Dichteänderungen bei solch langsamen Strömungen sehr gering ist. Dabei bedeutet Inkompressibilität, dass die Dichte räumlich homogen und zeitlich konstant ist: $$\begin{array}{r}\rho =\text{const.}\end{array}$$

Zudem kann, wegen der in sehr guter Näherung laminaren Strömung angenommen werden, dass diese stationär ist. Dies liegt daran, da die Reynolds-Zahl dem Verhältnis von Trägheitskräften, die versuchen das Fluid in Bewegung zu halten, zu viskosen Kräften, die Bewegungsunterschiede innerhalb des Fluides versuchen zu dämpfen, entspricht. Für Reynolds-Zahlen $\text{Re}\ll 1$ dominieren die viskosen Kräfte, was dazu führt, dass das Fluid in geordneten Schichten, ohne Querbewegung fließt. Aus der Stationärität des Fluids folgt, dann dass jede Zeitableitung von Größen, die dieses Fluid beschreiben, verschwinden.

Darüber hinaus kann, wegen obiger Argumentation, der Konvektionsterm $\rho (\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}$ vernachlässigt werden, da eben dieser die Trägheitskräfte beschreibt.

Mit der Annahme, dass keine externen Kräfte vorliegen, haben die zu lösenden Gleichungen dann folgende Form: $$\begin{array}{rl}& \overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u}=0\\ & \overrightarrow{\mathrm{\nabla }}p=\mu \mathrm{\Delta }\overrightarrow{u}\end{array}$$

Mit der Kontinuitätsgleichung für inkompressible Newtonsche Fluide folgt dann für den Spannungstensor: $$\begin{array}{r}\underset{―}{\underset{―}{\sigma }}=-p\mathbb{1}+\mu [\overrightarrow{\mathrm{\nabla }}\overrightarrow{u}+(\overrightarrow{\mathrm{\nabla }}\overrightarrow{u}{)}^T]\end{array}$$

Die zu lösenden Gleichungen sind nun analytisch lösbar. Es wird sich als sinnvoll herausstellen zunächst das Geschwindigkeitsfeld zu bestimmen. Dafür ist es nützlich die Rotation der Navier-Stokes-Gleichung zu betrachten. Denn mit der Tatsache, dass Gradientenfelder rotationsfrei sind, folgt: $$\begin{array}{r}\overrightarrow{\mathrm{\nabla }}\times (\mathrm{\Delta }\overrightarrow{u})=\mathrm{\Delta }(\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{u})=\overrightarrow{0}\end{array}$$

Aufgrund dessen, dass für das Geschwindigkeitsfeld im Unendlichen $\overrightarrow{u}(r\to \mathrm{\infty })$ gelten muss, lässt sich das Geschwindigkeitsfeld folgendermaßen schreiben: $$\begin{array}{r}\overrightarrow{u}={\overrightarrow{u}}^{\prime }+\overrightarrow{v}\end{array}$$

Dabei muss jedoch ${\overrightarrow{u}}^{\prime }$ im Unendlichen verschwinden.

Einsetzen in die Kontinuitätsgleichung liefert dann mit $\overrightarrow{v}=\text{const.}$: $$\begin{array}{r}\overrightarrow{\mathrm{\nabla }}\cdot {\overrightarrow{u}}^{\prime }=0\end{array}$$

Dies entspricht der notwendigen Bedingung für die Existenz eines Vektorpotentials $\overrightarrow{A}$ zu dem Vektorfeld ${\overrightarrow{u}}^{\prime }$. Daher lässt sich ${\overrightarrow{u}}^{\prime }$ folgendermaßen schreiben: $$\begin{array}{r}{\overrightarrow{u}}^{\prime }=\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{A}\end{array}$$

Da das Geschwindigkeitsfeld $\overrightarrow{u}$ und somit auch ${\overrightarrow{u}}^{\prime }$ und die Rotation eines polaren Vektors ein axialer Vektor ist und umgekehrt, muss das Vektorpotential ein axialer Vektor sein. Außerdem darf das Vektorpotential nur vom Ortsvektor $\overrightarrow{r}=r{\overrightarrow{e}}_r\$$, sowie der Einstromgeschwindigkeit $\overrightarrow{v}$ abhängen, da dieses über das Geschwindigkeitsfeld ${\overrightarrow{u}}^{\prime }$ bestimmt wird und ${\overrightarrow{u}}^{\prime }$ eben nur abhängig vom Ortsvektor und der Einstromgeschwindigkeit ist. Da sowohl der Ortsvektor, als auch die Einstromgeschwindigkeit polare Vektoren sind, muss das Vektorpotential in irgendeiner Form aus dem Vektorprodukt dieser beiden bestehen. Es bietet sich also an folgenden Ansatz für das Vektorpotential zu wählen: $$\begin{array}{r}\overrightarrow{A}=f^{\prime }(r){\overrightarrow{e}}_r\times \overrightarrow{v}=\overrightarrow{\mathrm{\nabla }}f(r)\times \overrightarrow{v}\end{array}$$

Dabei ist $f(r)$ eine skalare Funktion, welche nur vom Betrag des Ortsvektors $r$ abhängt. Damit folgt für das Geschwindigkeitsfeld ${\overrightarrow{u}}^{\prime }$: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}{\overrightarrow{u}}^{\prime }=\overrightarrow{\mathrm{\nabla }}\times (\overrightarrow{\mathrm{\nabla }}f(r)\times \overrightarrow{v}),\text{mit}\overrightarrow{v}=\text{const.}\Rightarrow \overrightarrow{\mathrm{\nabla }}\times (f\overrightarrow{v})=\overrightarrow{\mathrm{\nabla }}f\times \overrightarrow{v}\\ & \iff {\overrightarrow{u}}^{\prime }=\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{\mathrm{\nabla }}\times (f\overrightarrow{v})\end{array}$$

Einsetzen liefert für das Geschwindigkeitsfeld $\overrightarrow{u}$: $$\begin{array}{r}\overrightarrow{u}=\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{\mathrm{\nabla }}\times (f\overrightarrow{v})+\overrightarrow{v}\end{array}$$

Einsetzen in die Navier-Stokes-Gleichung und ausnutzen der Relation $\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{u}=-\mathrm{\Delta }(\overrightarrow{\mathrm{\nabla }}\times (f\overrightarrow{v}))$ liefert:$$\begin{array}{rl}& \phantom{\leftrightarrow ,}{\mathrm{\Delta }}^2(\overrightarrow{\mathrm{\nabla }}\times (f\overrightarrow{v}))=\overrightarrow{0},\text{mit}\overrightarrow{v}=\text{const.}\Rightarrow \overrightarrow{\mathrm{\nabla }}\times (f\overrightarrow{v})=\overrightarrow{\mathrm{\nabla }}f\times \overrightarrow{v}\\ & \iff {\mathrm{\Delta }}^2(\overrightarrow{\mathrm{\nabla }}f\times \overrightarrow{v})=\overrightarrow{0}\\ & \iff {\mathrm{\Delta }}^2(\overrightarrow{\mathrm{\nabla }}f)\times \overrightarrow{v}=\overrightarrow{0}\end{array}$$

Aufgrund dessen, dass obiger Ausdruck für alle Einstromgeschwindigkeiten gelten muss, muss insbesondere gelten: $$\begin{array}{r}{\mathrm{\Delta }}^2(\overrightarrow{\mathrm{\nabla }}f)=\overrightarrow{0}\end{array}$$

Eine erste Integration liefert dann: $$\begin{array}{r}{\mathrm{\Delta }}^{2}f=\text{const.}\end{array}$$

Da das Geschwindigkeitsfeld ${\overrightarrow{u}}^{\prime }$ im Unendlichen verschwinden muss, müssen auch dessen Ableitungen im Unendlichen verschwinden. Aufgrund dessen, dass ${\mathrm{\Delta }}^{2}f$ die vierten Ableitungen von $f$ enthält und das Geschwindigkeitsfeld ${\overrightarrow{u}}^{\prime }$ die zweiten Ableitungen von $f$ enthält, muss die Konstante Null sein. Damit folgt: $$\begin{array}{r}{\mathrm{\Delta }}^{2}f=0\end{array}$$

Da die Funktion $f(r)$ ausschließlich vom Betrag des Ortsvektors $r$ abhängt, reduziert sich der Laplace-Operator zu: $$\begin{array}{r}{\mathrm{\Delta }}^{2}f=\frac{1}{r^2}\frac{\partial }{\partial r}(r^2\frac{\partial }{\partial r})\mathrm{\Delta }f=0\end{array}$$

Damit ist $\mathrm{\Delta }f$ allgemein gegeben durch: $$\begin{array}{r}\mathrm{\Delta }f=\frac{2a}{r}+A,a,A\in \mathbb{R}\end{array}$$

Damit das Geschwindigkeitsfeld ${\overrightarrow{v}}^{\prime }$ im Unendlichen verschwindet, müssen alle additiven Konstanten gleich Null gewählt werden. Einsetzen liefert: $$\begin{array}{r}\mathrm{\Delta }f=\frac{2a}{r}\end{array}$$

Analoges Vorgehen zu oben liefert dann für die Funktion $f(r)$: $$\begin{array}{r}f(r)=ar+\frac{b}{r},a,b\in \mathbb{R}\end{array}$$

Einsetzen in $\overrightarrow{u}=\overrightarrow{u}=\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{\mathrm{\nabla }}\times (f\overrightarrow{v})+\overrightarrow{v}$ liefert dann: $$\begin{array}{r}\overrightarrow{u}=\overrightarrow{v}-a\frac{\overrightarrow{v}+(\overrightarrow{v}\cdot {\overrightarrow{e}}_r){\overrightarrow{e}}_r}{r}+b\frac{3(\overrightarrow{v}\cdot {\overrightarrow{e}}_r){\overrightarrow{e}}_r-\overrightarrow{v}}{r^3}\end{array}$$

Die Integrationskonstanten $a$ und $b$ lassen sich nun über die Randbedingung, dass das Geschwindigkeitsfeld auf der Kugeloberfläche verschwinden muss bestimmen. Es muss also gelten: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}\overrightarrow{u}(r=R)=\overrightarrow{0}\\ & \iff \overrightarrow{0}=\overrightarrow{v}-a\frac{\overrightarrow{v}+(\overrightarrow{v}\cdot {\overrightarrow{e}}_r){\overrightarrow{e}}_r}{r}+b\frac{3(\overrightarrow{v}\cdot {\overrightarrow{e}}_r){\overrightarrow{e}}_r-\overrightarrow{v}}{r^3}\\ & \iff \overrightarrow{0}=(-\frac{a}{R}-\frac{b}{R^3}+1)\overrightarrow{v}+(-\frac{a}{R}+\frac{3b}{R^3})(\overrightarrow{v}\cdot {\overrightarrow{e}}_r){\overrightarrow{e}}_r\end{array}$$

Aufgrund dessen, dass die obige Gleichung für alle $\overrightarrow{v}$ und alle ${\overrightarrow{e}}_r$ gelten muss, müssen deren Koeffizienten verschwinden. Daher sind die Integrationskonstanten gegeben durch: $$\begin{array}{r}a=\frac{3}{4}Rb=\frac{1}{4}{R}^3\end{array}$$

Damit ist das Geschwindigkeitsfeld endgültig gegeben durch: $$\begin{array}{r}\overrightarrow{u}=\overrightarrow{v}-\frac{3}{4}R\frac{\overrightarrow{v}+(\overrightarrow{v}\cdot {\overrightarrow{e}}_r){\overrightarrow{e}}_r}{r}-\frac{1}{4}{R}^3\frac{\overrightarrow{v}-3(\overrightarrow{v}\cdot {\overrightarrow{e}}_r){\overrightarrow{e}}_r}{r^3}\end{array}$$

Die jeweiligen Komponenten sind dann gegeben durch: $$\begin{array}{rl}& u_r=v\cos (\theta )(1-\frac{3R}{2r}+\frac{R^3}{2r^3})\\ & u_{\theta }=v\sin (\theta )(1-\frac{3R}{4r}-\frac{R^3}{4r^3})\\ & u_{\phi }=0\end{array}$$

Um nun das Druckfeld berechnen zu können, wird der Ausdruck $\overrightarrow{u}=\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{\mathrm{\nabla }}\times (f\overrightarrow{v})+\overrightarrow{v}$ in die Navier-Stokes-Gleichung eingesetzt und die Relation $\overrightarrow{\mathrm{\nabla }}\times \overrightarrow{\mathrm{\nabla }}\times (f\overrightarrow{v})=\overrightarrow{\mathrm{\nabla }}(\overrightarrow{\mathrm{\nabla }}f\cdot \overrightarrow{v})\overrightarrow{v}\mathrm{\Delta }f$ ausgenutzt: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}\overrightarrow{\mathrm{\nabla }}p=\mu \mathrm{\Delta }(\overrightarrow{\mathrm{\nabla }}(\overrightarrow{\mathrm{\nabla }}f\cdot \overrightarrow{v})-\overrightarrow{v}\mathrm{\Delta }f),\text{mit}{\mathrm{\Delta }}^{2}f=0\\ & \iff \overrightarrow{\mathrm{\nabla }}p=\mu \mathrm{\Delta }(\overrightarrow{\mathrm{\nabla }}(\overrightarrow{\mathrm{\nabla }}f\cdot \overrightarrow{v}))\\ & \iff \overrightarrow{\mathrm{\nabla }}p=\overrightarrow{\mathrm{\nabla }}(\mu \mathrm{\Delta }(\overrightarrow{\mathrm{\nabla }}f\cdot \overrightarrow{v}))\end{array}$$

Eine erste Integration liefert: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}p=\mu \mathrm{\Delta }(\overrightarrow{\mathrm{\nabla }}f\cdot \overrightarrow{v})+p_0\\ & \iff p=\mu \overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }}(\mathrm{\Delta }f)+p_0,\text{mit}f=\frac{3}{4}Rr+\frac{1}{4}\frac{R^3}{r}\\ & \iff p=p_0-\frac{3}{2r^2}\mu R\overrightarrow{v}\cdot {\overrightarrow{e}}_r\\ & \iff p=p_0+\frac{3}{2r^2}\mu vR\cos (\theta )\end{array}$$

Dabei ist $p_0$ der Druck des Fluides im Unendlichen. Nun kann also die Kraft auf die Kugel berechnet werden. Dabei gilt für ein Oberflächenelement $\text{d}\overrightarrow{A}$ einer Kugel mit Radius $r=R$, in Kugelkoordinaten: $$\begin{array}{r}d\overrightarrow{A}=R^2\sin (\theta )d\phi d\theta {\overrightarrow{e}}_r\end{array}$$

Einsetzen in obige Gleichung für die Kraft liefert dann: $$\begin{array}{r}\overrightarrow{F}={\int }_0^{\pi }{\int }_0^{2\pi }\underset{―}{\underset{―}{\sigma }}(r=R,\theta ,\phi )\cdot {\overrightarrow{e}}_r{R}^2\sin (\theta )d\phi d\theta \end{array}$$

Auswerten des Matrix-Vektor-Produktes liefert dann, dass nur die $rr$-, $\theta r$- und $\phi r$-Komponenten des Spannungstensors multipliziert mit entsprechenden Basisvektoren übrig bleiben. Es gilt also: $$\begin{array}{r}\overrightarrow{F}={\int }_0^{\pi }{\int }_0^{2\pi }[{\sigma }_{rr}{\overrightarrow{e}}_r+{\sigma }_{\theta r}{\overrightarrow{e}}_{\theta }+{\sigma }_{\phi r}{\overrightarrow{e}}_{\phi }]{|}_{r=R}{R}^2\sin (\theta )d\phi d\theta \end{array}$$

Die $rr$-Komponente des Spannungstensors ist dann gegeben durch: $$\begin{array}{r}{\sigma }_{rr}=-p+2\mu (\overrightarrow{\mathrm{\nabla }}\overrightarrow{u}{)}_{rr}\end{array}$$

$\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{rr}$ ist hier die $rr$-Komponente des Vektorgradienten $\overrightarrow{\mathrm{\nabla }}\overrightarrow{u}$, welche gegeben ist durch: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{rr}=\frac{\partial u_r}{\partial r},\text{mit}{u}_r=v\cos (\theta )(1-\frac{3R}{2r}+\frac{R^3}{2r^3})\\ & \iff \overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{rr}=0\end{array}$$

Mit $p=p_0+\frac{3}{2r^2}\mu vR\cos (\theta )$ folgt dann für $rr$-Komponente des Spannungstensors auf der Kugeloberfläche: $$\begin{array}{r}{\sigma }_{rr}{|}_{r=R}=-p_0-\frac{3}{2R}\mu v\cos (\theta )\end{array}$$

Für die $\theta r$-Komponente gilt dann gemäß obiger Gleichung: $$\begin{array}{r}{\sigma }_{\theta r}=\mu [\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{\theta r}+\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{r\theta }]\end{array}$$

Einsetzen der jeweiligen Komponenten des Vektorgradienten und auswerten an der Kugeloberfläche liefert: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}{\sigma }_{\theta r}{|}_{r=R}=\mu [\frac{\partial u_{\theta }}{\partial r}{|}_{r=R}+\frac{1}{R}\frac{\partial u_r}{\partial \theta }{|}_{r=R}-\frac{u_{\theta }}{R}{|}_{r=R}]\\ & \iff {\sigma }_{\theta r}{|}_{r=R}=\frac{3}{2R}\mu v\sin (\theta )\end{array}$$

Für die $\phi r$-Komponente gilt gemäß obiger Gleichung: $$\begin{array}{r}{\sigma }_{\phi r}=\mu [\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{\phi r}+\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{r\phi }]\end{array}$$

Einsetzen der jeweiligen Komponenten des Vektorgradienten und auswerten an der Kugeloberfläche liefert: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}{\sigma }_{\phi r}{|}_{r=R}=[\frac{\partial u_{\phi }}{\partial r}{|}_{r=R}+\frac{1}{R\sin (\theta )}\frac{\partial u_r}{\partial \phi }{|}_{r=R}-\frac{u_{\phi }}{R}{|}_{r=R}]\\ & \iff {\sigma }_{\phi r}{|}_{r=R}=0\end{array}$$

Damit folgt für die Kraft auf die umströmte Kugel: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}\overrightarrow{F}={\int }_0^{\pi }{\int }_0^{2\pi }[-p_0{\overrightarrow{e}}_r-\frac{3}{2R}\mu v\cos (\theta ){\overrightarrow{e}}_r+\frac{3}{2R}\mu v\sin (\theta ){\overrightarrow{e}}_{\theta }]{|}_{r=R}{R}^2\sin (\theta )d\phi d\theta \\ & \iff \overrightarrow{F}=6\pi \mu R\overrightarrow{v}\end{array}$$

Oseen'sche Näherung

Bei der Herleitung der Stokes'schen Formel wurden Annahmen getroffen, die für sehr kleine Reynolds-Zahlen $\text{Re}\ll 1$ gültig sind. Oseen schaffte es nun eine erste Näherung für kleine Reynolds-Zahlen $\text{Re}<1$ zu formulieren, indem er den Konvektionsterm, in linearer Form, berücksichtigt. Aufgrund dessen, dass in der Oseen'schen Näherung immer noch vergleichsweise kleine Reynolds-Zahlen betrachtet werden, kann weiterhin von einer stationären Strömung ausgegangen werden. Des weiteren kann, wegen der vergleichsweise kleinen Reynolds-Zahlen weiterhin von einem inkompressiblen Fluid ausgegangen werden. Mit diesen Annahmen folgt für die Navier-Stokes-Gleichung: $$\begin{array}{r}\rho (\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}=-\overrightarrow{\mathrm{\nabla }}p+\mu \mathrm{\Delta }\overrightarrow{u}\end{array}$$

Um nun den Konvektionsterm linearisieren zu können, wird analog zu oben davon ausgegangen, dass sich das Geschwindigkeitsfeld folgendermaßen schreiben lässt: $$\begin{array}{r}\overrightarrow{u}={\overrightarrow{u}}^{\prime }+\overrightarrow{v},\text{mit}{\overrightarrow{u}}^{\prime }(r\to \mathrm{\infty })=\overrightarrow{0}\end{array}$$

Einsetzen in den Konvektionsterm liefert: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}(\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}=(({\overrightarrow{u}}^{\prime }+\overrightarrow{v})\cdot \overrightarrow{\mathrm{\nabla }})({\overrightarrow{u}}^{\prime }+\overrightarrow{v})\\ & \iff (\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}=({\overrightarrow{u}}^{\prime }\cdot \overrightarrow{\mathrm{\nabla }}){\overrightarrow{u}}^{\prime }+({\overrightarrow{u}}^{\prime }\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{v}+(\overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }}){\overrightarrow{u}}^{\prime }+(\overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{v},\text{mit}\overrightarrow{v}=\text{const.}\\ & \iff (\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}=({\overrightarrow{u}}^{\prime }\cdot \overrightarrow{\mathrm{\nabla }}){\overrightarrow{u}}^{\prime }+(\overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }}){\overrightarrow{u}}^{\prime }\end{array}$$

Da hier weiterhin kleine Reynolds-Zahlen betrachtet werden, kann davon ausgegangen werden, dass die Störung ${\overrightarrow{u}}^{\prime }$ klein ist, sodass Terme zweiter Ordnung, wie $({\overrightarrow{u}}^{\prime }\cdot \overrightarrow{\mathrm{\nabla }}){\overrightarrow{u}}^{\prime }$ vernachlässigt werden können. Damit folgt für den linearisierten Konvektionsterm: $$\begin{array}{r}(\overrightarrow{u}\cdot \overrightarrow{\mathrm{\nabla }})\overrightarrow{u}=(\overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }}){\overrightarrow{u}}^{\prime }\end{array}$$

Damit folgt für die Navier-Stokes-Gleichung: $$\begin{array}{r}\rho (\overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }}){\overrightarrow{u}}^{\prime }=-\overrightarrow{\mathrm{\nabla }}p+\mu \mathrm{\Delta }{\overrightarrow{u}}^{\prime }\end{array}$$

Die zu lösenden Gleichungen sind also gegeben durch: $$\begin{array}{rl}& \overrightarrow{\mathrm{\nabla }}\cdot {\overrightarrow{u}}^{\prime }=0\\ & \rho (\overrightarrow{v}\cdot \overrightarrow{\mathrm{\nabla }}){\overrightarrow{u}}^{\prime }=-\overrightarrow{\mathrm{\nabla }}p+\mu \mathrm{\Delta }{\overrightarrow{u}}^{\prime }\end{array}$$

Lösen der Gleichungen und berechnen der Kraft gemäß $\overrightarrow{F}={\oint }_{\partial V}\underset{―}{\underset{―}{\sigma }}\cdot d\overrightarrow{A}$ liefert dann eine Korrektur zweiter Ordnung für die Stokes'sche Formel: $$\begin{array}{r}\overrightarrow{F}=6\pi \mu R\overrightarrow{u}(1+\frac{3}{8}\mathrm{Re})\end{array}$$

Numerische Berechnung der Kraft auf die Kugel

Im Unterschied zu der Annahme, die für die analytische Herleitung getroffen wurde, simuliert das verwendete Simulationsprogramm PLUTO kompressible Newtonsche Fluide. Damit verschwindet die Divergenz des Geschwindigkeitsfeldes nicht mehr, weshalb der Spannungstensor für solche Fluide gegeben ist durch: $$\begin{array}{r}\underset{―}{\underset{―}{\sigma }}=p\mathbb{1}+\mu [\overrightarrow{\mathrm{\nabla }}\overrightarrow{u}+(\overrightarrow{\mathrm{\nabla }}\overrightarrow{u}{)}^T-\frac{2}{3}(\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u})\mathbb{1}]\end{array}$$

Für die Kraft sind dabei jedoch nur die $rr$-, $\theta r$- und $\varphi r$-Komponenten des Spannungstensors von Interesse. Die $rr$-Komponente ist dabei gegeben durch: $$\begin{array}{r}{\sigma }_{rr}=-p+\mu [2\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{rr}-\frac{2}{3}\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u}]\end{array}$$

$\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{rr}$ ist hier die $rr$-Komponente des Vektorgradienten $\overrightarrow{\mathrm{\nabla }}\overrightarrow{u}$, welche gegeben ist durch: $$\begin{array}{r}\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{rr}=\frac{\partial u_r}{\partial r}\end{array}$$

Für die Divergenz des Geschwindigkeitsfeldes gilt allgemein in Kugelkoordinaten: $$\begin{array}{r}\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u}=\frac{1}{r^2}\frac{\partial r^2{u}_r}{\partial r}+\frac{1}{r\sin (\theta )}\frac{\partial \sin (\theta )u_{\theta }}{\partial \theta }+\frac{1}{r\sin (\theta )}\frac{\partial u_{\phi }}{\partial \phi }\end{array}$$

Aufgrund dessen, dass das Fluid homogen einströmt und eine Kugel umströmt, hat das Geschwindigkeitsfeld um die Kugel Zylindersymmetrie. Daher fällt die azimutale Ableitung bei Betrachtung des Geschwindigkeitsfeldes um die Kugel weg. Außerdem folgt aus der vorgegebenen Anfangsbedingung, dass das Fluid entlang der z-Achse einströmt, zusammen mit der Kugelsymmetrie der Kugel, dass das Geschwindigkeitsfeld und auch sämtliche anderen relevanten Vektorfelder, die dieses Problem beschreiben, keine azimutale Komponente aufweisen können. Damit folgt für die Divergenz des Geschwindigkeitsfeldes:

$$\begin{array}{r}\overrightarrow{\mathrm{\nabla }}\cdot \overrightarrow{u}=\frac{1}{r^2}\frac{\partial r^2{u}_r}{\partial r}+\frac{1}{r\sin (\theta )}\frac{\partial \sin (\theta )u_{\theta }}{\partial \theta }\end{array}$$

Einsetzen in die $rr$-Komponente und auswerten an der Kugeloberfläche liefert: $$\begin{array}{r}{\sigma }_{rr}{|}_{r=R}=-p+\mu [2\frac{\partial u_r}{\partial r}{|}_{r=R}-\frac{2}{3}\frac{1}{R^2}\frac{\partial r^2{u}_r}{\partial r}{|}_{r=R}+\frac{1}{R\sin (\theta )}\frac{\partial \sin (\theta )u_{\theta }}{\partial \theta }{|}_{r=R}]\end{array}$$

Die Ableitungen lassen sich zusätzlich mittels der Produktregel vereinfachen. Es folgt: $$\begin{array}{r}{\sigma }_{rr}{|}_{r=R}=-p+\mu [\frac{4}{3}\frac{\partial u_r}{\partial r}{|}_{r=R}-\frac{4}{3R}{u}_r{|}_{r=R}-\frac{2}{3R}\cot (\theta )u_{\theta }{|}_{r=R}-\frac{2}{3R}\frac{\partial u_{\theta }}{\partial \theta }{|}_{r=R}]\end{array}$$

Mit den Randbedingungen folgt, dass für das Geschwindigkeitsfeld gelten muss: $$\begin{array}{r}{u}_r{|}_{r=R}=u_{\theta }{|}_{r=R}=0\end{array}$$

Außerdem impliziert das Verschwinden der Geschwindigkeitsvektoren auf der Kugeloberfläche und dessen Kugelsymmetrie, dass zusätzlich die polaren Ableitungen auf der Oberfläche verschwinden: $$\begin{array}{r}\frac{\partial u_r}{\partial \theta }{|}_{r=R}=\frac{\partial u_{\theta }}{\partial \theta }{|}_{r=R}=0\end{array}$$

Damit folgt für die $rr$-Komponente des Spannungstensors, ausgewertet an der Kugeloberfläche: $$\begin{array}{r}{\sigma }_{rr}{|}_{r=R}=-p+\frac{4}{3}\mu \frac{\partial u_r}{\partial r}{|}_{r=R}\end{array}$$

Für die $\theta r$-Komponente gilt analog zu oben: $$\begin{array}{r}{\sigma }_{\theta r}=\mu [\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{\theta r}+\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{r\theta }]\end{array}$$

Einsetzen der jeweiligen Komponenten des Vektorgradienten und auswerten an der Kugeloberfläche liefert: $$\begin{array}{r}{\sigma }_{\theta r}{|}_{r=R}=\mu [\frac{\partial u_{\theta }}{\partial r}{|}_{r=R}+\frac{1}{R}\frac{\partial u_r}{\partial \theta }{|}_{r=R}-\frac{u_{\theta }}{R}{|}_{r=R}]\end{array}$$

Ausnutzen der Randbedingungen liefert dann: $$\begin{array}{r}{\sigma }_{\theta r}{|}_{r=R}=\mu \frac{\partial u_{\theta }}{\partial r}{|}_{r=R}\end{array}$$

Für die $\phi r$-Komponente gilt gemäß obiger Gleichung: $$\begin{array}{r}{\sigma }_{\phi r}=\mu [\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{\phi r}+\overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{r\phi }]\end{array}$$

Die jeweiligen Komponenten des Vektorgradienten sind im Allgemeinen gegeben durch: $$\begin{array}{rl}& \overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{\phi r}=\frac{\partial u_{\phi }}{\partial r}\\ & \overrightarrow{\mathrm{\nabla }}{\overrightarrow{u}}_{r\phi }=\frac{1}{r\sin (\theta )}\frac{\partial u_r}{\partial \phi }-\frac{u_{\phi }}{r}\end{array}$$

Analog zu oben fallen hier auch sowohl die azimutalen Komponenten als auch die azimutalen Ableitungen weg, weshalb für die $\phi r$-Komponente des Spannungstensors folgt: $$\begin{array}{r}{\sigma }_{\phi r}=0\end{array}$$

Einsetzen in das Integral zur Kraftberechnung und auswerten des Integrals über $\phi$ liefert: $$\begin{array}{rl}& \phantom{\leftrightarrow ,,}\overrightarrow{F}=2\pi R^2{\int }_0^{\pi }[(-p+\frac{4}{3}\mu \frac{\partial u_r}{\partial r}{|}_{r=R}){\overrightarrow{e}}_r+\mu \frac{\partial u_{\theta }}{\partial r}{|}_{r=R}{\overrightarrow{e}}_{\theta }]\sin (\theta )\text{d}\theta \\ & \iff \overrightarrow{F}=2\pi R^2[-{\int }_0^{\pi }p{\overrightarrow{e}}_r\sin (\theta )d\theta +\frac{4}{3}{\int }_0^{\pi }\mu \frac{\partial u_r}{\partial r}{|}_{r=R}{\overrightarrow{e}}_r\sin (\theta )\text{d}\theta +{\int }_0^{\pi }\mu \frac{\partial u_{\theta }}{\partial r}{|}_{r=R}{\overrightarrow{e}}_{\theta }\sin (\theta )\text{d}\theta ]\end{array}$$

Da im vorliegenden Problem insbesondere die Kraft auf die Kugel in $z$-Richtung von Interesse ist, wird nun die Projektion des Kraftvektors auf die z-Achse bestimmt: $$\begin{array}{r}{F}_z={\overrightarrow{e}}_z\cdot \overrightarrow{F}\end{array}$$

Aufgrund dessen, dass die $z$-Achse eine feste Richtung hat und der Linearität der Integrationsoperation, kann der Basisvektor ${\overrightarrow{e}}_z$ in das Integral hineingezogen werden. Damit folgt für $F_z$: $$\begin{array}{rl}& F_z=2\pi R^2[-{\int }_0^{\pi }p{\overrightarrow{e}}_r\cdot {\overrightarrow{e}}_z\sin (\theta )d\theta +\frac{4}{3}{\int }_0^{\pi }\mu \frac{\partial u_r}{\partial r}{|}_{r=R}{\overrightarrow{e}}_r\cdot {\overrightarrow{e}}_z\sin (\theta )\text{d}\theta \\ & \phantom{\leftrightarrow ,,}+{\int }_0^{\pi }\mu \frac{\partial u_{\theta }}{\partial r}{|}_{r=R}{\overrightarrow{e}}_{\theta }\cdot {\overrightarrow{e}}_z\sin (\theta )\text{d}\theta ]\end{array}$$

Für die Berechnung der jeweiligen Skalarprodukte ist es praktisch den Basisvektor ${\overrightarrow{e}}_z$ in der hier genutzten sphärischen Basis darzustellen: $$\begin{array}{r}{\overrightarrow{e}}_z=\cos (\theta ){\overrightarrow{e}}_r-\sin (\theta ){\overrightarrow{e}}_{\theta }\end{array}$$

Damit folgt für $F_z$: $$\begin{array}{rl}& F_z=2\pi R^2[-{\int }_0^{\pi }p\cos (\theta )\sin (\theta )d\theta +\frac{4}{3}{\int }_0^{\pi }\mu \frac{\partial u_r}{\partial r}{|}_{r=R}\cos (\theta )\sin (\theta )\text{d}\theta \\ & \phantom{\leftrightarrow ,,}-{\int }_0^{\pi }\mu \frac{\partial u_{\theta }}{\partial r}{|}_{r=R}{\sin }^2(\theta )\text{d}\theta ]\end{array}$$

Die Kraft in $x$- bzw. $y$-Richtung lässt sich analog berechnen. Da jedoch die Basisvektoren ${\overrightarrow{e}}_x$ bzw. ${\overrightarrow{e}}_y$ in sphärischer Darstellung eine $\phi$-Abhängigkeit aufweisen, kann die Integration über $\phi$ nicht so leicht durchgeführt werden, wie es oben geschehen ist. Für die Kraft in $x$-Richtung muss dann folgendes Integral ausgewertet werden: $$\begin{array}{rl}& F_x=R^2[-{\int }_0^{\pi }{\int }_0^{2\pi }p(R,\theta ){\sin }^2(\theta )\cos (\phi )d\phi d\theta +\frac{4}{3}{\int }_0^{\pi }{\int }_0^{2\pi }\mu (R,\theta )\frac{\partial u_r}{\partial r}{|}_{r=R}{\sin }^2(\theta )\cos (\phi )d\phi d\theta \\ & \phantom{\leftrightarrow ,,}+{\int }_0^{\pi }{\int }_0^{2\pi }\mu (R,\theta )\frac{\partial u_{\theta }}{\partial r}{|}_{r=R}\sin (\theta )\cos (\theta )\cos (\phi )d\phi d\theta ]\end{array}$$

Auswerten der Integrale über $\phi$ liefert jedoch, wie zu erwarten war, für $F_x$: $$\begin{array}{r}{F}_x=0\end{array}$$

Analoges Vorgehen liefert für $F_y$: $$\begin{array}{r}{F}_y=0\end{array}$$

Numerische Integration

Da PLUTO die Daten nur für die jeweiligen Zellzentren ausgibt, werden insbesondere keine Daten an der Kugeloberfläche ausgegeben. Diese Daten sind jedoch gemäß der obigen Formel zur Berechnung der Kraft erforderlich. Das Geschwindigkeitsfeld an der Kugeloberfläche ist jedoch bereits aus den Randbedingungen bekannt: $$\begin{array}{r}\overrightarrow{u}(r=R,\theta )=\overrightarrow{0}\mathrm{\forall }\theta \in [0,\pi ]\end{array}$$

Der Druck auf der Kugeloberfläche ist jedoch unbekannt und muss daher extrapoliert werden. Eine lineare Extrapolation bietet sich an, da sie einen Fehler zweiter Ordnung aufweist, welcher mit den Fehlern der verwendeten Methoden zur Bestimmung der Ableitungen der Felder übereinstimmt. Zudem ist eine lineare Extrapolation ausreichend, da bei einer ausreichend hohen Gitterauflösung die Zellzentren der Zellen in der ersten Zellschale um die Kugeloberfläche nicht weit von dieser entfernt sind. Für die lineare Extrapolation des Drucks auf die Kugeloberfläche $p(r=R)=p_0$ werden die beiden nächsten Datenpunkte $(r_1,p_1)$ und $(r_2,p_2)$ benötigt. Der extrapolierte Druck ist dann gegeben durch: $$\begin{array}{r}{p}_0=p_2+\frac{R-r_2}{r_1-r_2}(p_1-p_2)\end{array}$$

Aufgrund dessen, dass die Daten jedoch keine kontinuierlichen Größen sind, kann das für die Kraftberechnung benötigte Integral nur näherungsweise berechnet werden. Obiges Integral ist dabei ein Integral über den Polarwinkel $\theta$ über eine Funktion $f(\theta )$, welche nur von diesem Winkel abhängt. Um das Integral also zu nähern, wird der obige Integrand $f({\theta }_i)$ in jeder Zelle für den Winkel $\theta_i$ ausgewertet und dann Gewichtet mit der jeweiligen Breite der Zelle $\mathrm{\Delta }{\theta }_i$ in polarer Richtung, über alle $N_{\theta }$ aufsummiert: $$\begin{array}{r}{\int }_0^{\pi }f(\theta )d\theta \to \sum _{i}f({\theta }_i)\mathrm{\Delta }{\theta }_i\end{array}$$

Aufgrund dessen, dass die polare Aufteilung der Zellen in vorliegendem Gitter uniform gewählt wurde gilt: $$\begin{array}{r}\mathrm{\Delta }{\theta }_i=\mathrm{\Delta }{\theta }_j=\mathrm{\Delta }\theta \mathrm{\forall }i,j\in [0,N_{\theta }-1]\end{array}$$

Damit folgt: $$\begin{array}{r}{\int }_0^{\pi }f(\theta )d\theta \to \sum _{i}f({\theta }_i)\mathrm{\Delta }\theta \end{array}$$

Kompression des Fluides

Wie oben angemerkt, simuliert das verwendete Simulationsprogramm PLUTO kompressible Fluide. Die Stokes'sche Formel wurde jedoch unter der Annahme, dass es sich bei dem vorliegenden Fluid um ein inkompressibles Fluid handelt, hergeleitet.

Um die Vergleichbarkeit mit der analytisch hergeleiteten Formel sicherzustellen, muss also die Kompression des Fluides bezüglich einer Reynolds-Zahl-Veränderung konstant und klein sein. Ein Maß für die Kompression eines Fluides ist die relative Massenänderung $\delta m_{\mathrm{rel}}$ in einem beliebigen, aber festen Volumen $V$ um die Kugel, für den Fall, das mit einem kompressiblen Fluid, anstatt mit einem inkompressiblen Fluid auf die Kugel eingeströmt wird. Die relative Massenänderung ist dabei definiert durch: $$\begin{array}{r}\delta m_{\mathrm{rel}}=\frac{m-\tilde{m}}{\tilde{m}}\end{array}$$

Dabei bezeichnet $m$ die Masse des kompressiblen Fluids innerhalb des betrachteten Volumens, während $\tilde{m}$ die Masse des inkompressiblen Fluids innerhalb desselben Volumens darstellt.

Damit die Kompression des betrachteten Fluides bezüglich einer Reynolds-Zahl-Veränderung konstant ist, muss also die relative Massenänderung innerhalb des betrachteten Volumens konstant bezüglich einer Reynolds-Zahl-Veränderung sein. Es muss also gelten: $$\begin{array}{r}\delta m_{\mathrm{rel}}=\mathrm{const}.\end{array}$$

Gesucht ist also nun ein expliziter Zusammenhang, damit die Kompression bezüglich einer Reynolds-Zahl-Veränderung eine Konstante ist. Dabei erweist es sich als sinnvoll, die relative Dichteänderung $\delta {\rho }_{\mathrm{rel}}$ zu betrachten. Diese ist analog zur relativen Massenänderung definiert durch: $$\begin{array}{r}\delta {\rho }_{\mathrm{rel}}=\frac{\rho -\tilde{\rho }}{\tilde{\rho }}\end{array}$$

Dabei sind $\rho$ bzw. $\tilde{\rho }$ die entsprechenden Dichtefelder des kompressiblen bzw. inkompressiblen Fluides. Dies ist auch der zentrale Unterschied zwischen der relativen Massenänderung und der relativen Dichteänderung. Denn während die relative Massenänderung ein Skalar ist, ist die relative Dichteänderung ein skalares Feld ist. Es gilt also: $$\begin{array}{r}\delta {\rho }_{\mathrm{rel}}=\delta {\rho }_{\mathrm{rel}}(\overrightarrow{r}),\text{mit}\overrightarrow{r}\in V\end{array}$$

Damit also nun die relative Massenänderung bezüglich einer Reynolds-Zahl-Veränderung eine Konstante beschreibt, lässt sich zeigen, dass die relative Dichteänderung lokal konstant und insbesondere unabhängig von der Reynolds-Zahl sein muss. Es gilt also: $$\begin{array}{r}\delta {\rho }_{\mathrm{rel}}(\overrightarrow{r})=c(\overrightarrow{r}),\text{mit}c(\overrightarrow{r})\in \mathbb{R}\end{array}$$

Diese Implikation lässt sich durch die folgende Rechnung veranschaulichen: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}\delta {\rho }_{\mathrm{rel}}(\overrightarrow{r})=c(\overrightarrow{r})\\ & \iff \frac{\rho (\overrightarrow{r})-\tilde{\rho }}{\tilde{\rho }}=c(\overrightarrow{r})\end{array}$$

Hierbei ist das Dichtefeld des inkompressiblen Fluids, wie in der analytischen Herleitung der Stokes'schen Formel erwähnt, homogen und somit ortsunabhängig. Wird das ortsabhängige Feld $c(\overrightarrow{r})$ mit dem homogenen Dichtefeld des inkompressiblen Fluids multipliziert, so bleibt das resultierende Feld $c^{\prime }(\overrightarrow{r})$ weiterhin ortsabhängiges. Damit folgt: $$\begin{array}{r}\rho (\overrightarrow{r})-\tilde{\rho }=c^{\prime }(\overrightarrow{r})\end{array}$$

Integration über das betrachtete Volumen liefert dann: $$\begin{array}{r}m-\tilde{m}=C,\text{mit}C\in \mathbb{R}\end{array}$$

Dividieren durch die Masse des inkompressiblen Fluides innerhalb des betrachteten Volumens ändert jedoch nichts daran, dass die Gleichung konstant bleibt: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}\frac{m-\tilde{m}}{\tilde{m}}=\mathrm{const}.\\ & \iff \delta m_{\mathrm{rel}}=\mathrm{const}.\end{array}$$

Um nun einen expliziten Zusammenhang finden zu können, unter dem die Kompression bezüglich einer Reynolds-Zahl-Veränderung eine Konstante beschreibt, wird im folgenden die Differenz $\rho -\tilde{\rho }$ betrachtet. Dafür wird zunächst die Dichte des kompressiblen Fluides, um den Druck des Systems im Unendlichen $p_{\mathrm{\infty }}$ bis zur linearen Ordnung entwickelt. Dabei wird ausgenutzt, dass bei Strömungen, weit im laminaren Regime, keine großen Druckänderungen auftreten können, weshalb das vorliegende Druckfeld folgendermaßen geschrieben werden kann: $$\begin{array}{r}p=p_{\mathrm{\infty }}+p^{\prime }\end{array}$$

Hierbei beschreibt $p^{\prime }$ die entsprechende Störung des Druckfeldes im Unendlichen. Für Strömungen, weit im laminaren Regime, muss dann für die Störung gelten: $$\begin{array}{r}{p}^{\prime }\ll p_{\mathrm{\infty }}\end{array}$$

Entwickeln der Dichte des kompressiblen Fluides, um den Druck des Systems im Unendlichen liefert dann: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}\rho (p=p_{\mathrm{\infty }}+p^{\prime })=\rho (p_{\mathrm{\infty }})+\frac{\partial \rho }{\partial p}{|}_{p=p_{\mathrm{\infty }}}(p-p_{\mathrm{\infty }})+\mathcal{O}((p-p_{\mathrm{\infty }}{)}^2)\\ & \iff \rho (p=p_{\mathrm{\infty }}+p^{\prime })=\rho (p_{\mathrm{\infty }})+\frac{\partial \rho }{\partial p}{|}_{p=p_{\mathrm{\infty }}}{p}^{\prime }+\mathcal{O}(p^{\prime 2})\end{array}$$

Gesucht sind nun die Dichte $\rho (p_{\mathrm{\infty }})$ ausgewertet an dem Druck im Unendlichen und die Ableitung der Dichte nach dem Druck, ebenfalls ausgewertet an dem Druck im Unendlichen.

Dabei kann für die Dichte, ausgewertet am Druck im Unendlichen genutzt werden, dass sie der Dichte eines inkompressiblen Fluides entspricht. Dies liegt daran, dass die Dichte des kompressiblen Fluides, ausgewertet am Druck im Unendlichen, äquivalent zu der Dichte in einem Szenario ist, in dem nicht auf die Kugel eingestrahlt wird, also in dem $v=0$ gilt. In Abwesenheit dieser Einstrahlung treten keine Dichteänderungen auf, wodurch dieser Fall dem eines inkompressiblen Fluids entspricht. Folglich gilt: $$\begin{array}{r}\rho (p_{\mathrm{\infty }})={\rho }_{\mathrm{\infty }}=\tilde{\rho }\end{array}$$

Dabei ist ${\rho }_{\mathrm{\infty }}$ die Dichte des Fluides im Unendlichen.

Für die gesuchte Ableitung der Dichte nach dem Druck bietet es sich an die Kompressibilität $\beta$ eines Fluides einzuführen. Die Kompressibilität eines Fluides ist dabei ein Maß dafür, wie sehr das Volumen des Fluides komprimiert werden kann. Sie wird definiert durch die relative Volumenänderung pro Einheitsdruckänderung: $$\begin{array}{r}\beta =-\frac{1}{V}\frac{\partial V}{\partial p}\end{array}$$

Die Kompressibilität lässt sich jedoch auch über die relative Dichteänderung pro Einheitsdruckänderung definieren: $$\begin{array}{r}\beta =\frac{1}{\rho }\frac{\partial \rho }{\partial p}\end{array}$$

Dabei sind beide Definitionen äquivalent und beschreiben demnach die selbe physikalische Größe. Dies kann durch eine einfache Rechnung veranschaulicht werden. Dabei wird von der Volumenkompressibilität ${\beta }_V$ ausgegangen: $$\begin{array}{r}{\beta }_V=-\frac{1}{V}\frac{\partial V}{\partial p}\end{array}$$

Aufgrund dessen, dass die Kompressibilität eine lokale Größe ist, kann angenommen werden, dass die Dichte $\rho$ in einem Kontrollvolumen $V$ gegeben ist durch: $$\begin{array}{r}\rho =\frac{m}{V}\end{array}$$

Dabei ist $m$ die Masse des Fluides in diesem Kontrollvolumen. Umformen liefert: $$\begin{array}{r}V=\frac{m}{\rho }\end{array}$$

Einsetzen in die Volumenkompressibilität liefert: $$\begin{array}{r}{\beta }_V=-\frac{1}{V}\frac{\partial }{\partial p}(\frac{m}{\rho })\end{array}$$

Ausnutzen, dass die Masse eines Fluides unter Druckänderung konstant bleibt, und Anwenden der Kettenregel liefert: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}{\beta }_V=-\frac{m}{V}\frac{\partial }{\partial \rho }(\frac{1}{\rho })\frac{\partial \rho }{\partial p}\\ & \iff {\beta }_V=\frac{1}{\rho }\frac{\partial \rho }{\partial p},\text{mit}{\beta }_{\rho }=\frac{1}{\rho }\frac{\partial \rho }{\partial p}\\ & \iff {\beta }_V={\beta }_{\rho }=:\beta \end{array}$$

Andererseits lässt sich die Kompressibilität als Funktion der Schallgeschwindigkeit $c_S$ in dem Fluid ausdrücken. Denn die Schallgeschwindigkeit ist im Allgemeinen gegeben durch: $$\begin{array}{r}{c}_S=\sqrt{\frac{\partial p}{\partial \rho }}\end{array}$$

Damit folgt für die Kompressibilität als Funktion der Schallgeschwindigkeit: $$\begin{array}{r}\beta =\frac{1}{\rho c_S^2}\end{array}$$

Damit lässt sich nun die gesuchte Ableitung folgendermaßen schreiben: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}\frac{\partial \rho }{\partial p}{|}_{p=p_{\mathrm{\infty }}}=\beta (p_{\mathrm{\infty }})\rho (p_{\mathrm{\infty }}),\text{mit}\beta (p_{\mathrm{\infty }})=\frac{1}{\rho (p_{\mathrm{\infty }})c_S^2(p_{\mathrm{\infty }})}\\ & \iff \frac{\partial \rho }{\partial p}{|}_{p=p_{\mathrm{\infty }}}=\frac{1}{c_S^2(p_{\mathrm{\infty }})},\text{mit}{c}_S(p_{\mathrm{\infty }})=c_{S,\mathrm{\infty }}\\ & \iff \frac{\partial \rho }{\partial p}{|}_{p=p_{\mathrm{\infty }}}=\frac{1}{c_{S,\mathrm{\infty }}^2}\end{array}$$

Dabei ist $c_{S,\mathrm{\infty }}$ die Schallgeschwindigkeit des Fluides im Unendlichen.

Einsetzen in die Taylor-Entwicklung der Dichte des kompressiblen Fluides liefert:$$\begin{array}{r}\rho (p=p_{\mathrm{\infty }}+p^{\prime })=\tilde{\rho }+\frac{p^{\prime }}{c_{S,\mathrm{\infty }}^2}+\mathcal{O}(p^{\prime 2})\end{array}$$

Damit folgt für die relative Dichteänderung in einer Näherung erster Ordnung: $$\begin{array}{r}\delta {\rho }_{\mathrm{rel}}(\overrightarrow{r})=\frac{p^{\prime }(\overrightarrow{r})}{\tilde{\rho }{c}_{S,\mathrm{\infty }}^2}\end{array}$$

Aus der analytischen Herleitung der Stokes'schen Formel folgt zusätzlich folgende Proportionalität: $$\begin{array}{r}{p}^{\prime }(\overrightarrow{r})\propto v\mathrm{\forall }\overrightarrow{r}\end{array}$$

Ausnutzen dieser Proportionalität und der Konstanz der Dichte des inkompressiblen Fluides liefert dann für die ortsabhängige Konstante: $$\begin{array}{r}\frac{v}{c_{S,\mathrm{\infty }}^2}\propto c(\overrightarrow{r})\end{array}$$

Damit folgt, dass an einem beliebigen, aber festem Ort im betrachteten Volumen folgende Proportionalität gelten muss: $$\begin{array}{r}{c}_{S,\mathrm{\infty }}\propto \sqrt{v}\end{array}$$

Aufgrund dessen, dass die relative Dichteänderung für alle Orte in erster Ordnung gleich skaliert, gilt diese Proportionalität für alle Orte im betrachteten Volumen.

Daraus folgt, dass die Schallgeschwindigkeit im Unendlichen folgendermaßen skalieren muss, damit die Kompression des betrachteten Fluides bezüglich einer Reynolds-Zahl-Veränderung konstant ist: $$\begin{array}{r}{c}_{S,\mathrm{\infty }}=\alpha \sqrt{v}\end{array}$$

Dabei ist $\alpha$ ein Proportionalitätskonstante, welche zunächst frei gewählt werden kann.

Natürliche Einheiten

In der Physik und insbesondere bei der Durchführung von Experimenten ist es üblich, numerische Ergebnisse in SI-Einheiten auszudrücken. SI-Einheiten bieten eine universelle Grundlage, die es ermöglicht, experimentelle Daten und theoretische Ergebnisse konsistent und vergleichbar zu machen. Allerdings kann die Verwendung von SI-Einheiten bei theoretischen Berechnungen zu komplexen und schwer überschaubaren Gleichungen führen. Um diese Berechnungen zu vereinfachen und vergleichbarer zu gestalten, werden sogenannte natürliche Einheiten verwendet. Natürliche Einheiten sind speziell gewählte Maßeinheiten, die an die charakteristischen Größen der untersuchten physikalischen Systeme angepasst sind. Ein wesentlicher Vorteil dieser Einheiten ist die Vereinfachung physikalischer Gleichungen. Durch die geeignete Wahl von natürlichen Einheiten können viele physikalische Konstanten auf $1$ gesetzt werden, was die Anzahl der in den Gleichungen auftretenden Konstanten erheblich reduziert. Das Ziel bei der Verwendung natürlicher Einheiten besteht darin, die betreffenden Gleichungen dimensionslos zu machen. Für das gegebene Problem werden die relevanten Größen in Einheiten der Dichte im Unendlichen ${\rho }_{\mathrm{\infty }}$, der dynamischen Viskosität $\mu$ und des Objektradius $R$ gemessen. Bei der Wahl der natürlichen Einheiten ist es entscheidend, dass diese die physikalisch relevanten Dimensionen korrekt reproduzieren. Die Massen-, Längen- und Zeiteinheiten in natürlichen Einheiten sind dann gegeben durch: $$\begin{array}{r}{\rho }_{\mathrm{\infty }}{R}^3,R,\frac{{\rho }_{\mathrm{\infty }}{R}^2}{\mu }\end{array}$$

Mit der Definition der Reynolds-Zahl ergibt sich für die Einstromgeschwindigkeit in den gewählten natürlichen Einheiten: $$\begin{array}{r}\frac{v}{\mu /({\rho }_{\mathrm{\infty }}R)}=\frac{\text{Re}\mu /(2{\rho }_{\mathrm{\infty }}R)}{\mu /({\rho }_{\mathrm{\infty }}R)}=\frac{\text{Re}}{2}\end{array}$$

Da die Reynolds-Zahl eine dimensionslose Größe ist, ist die Einstromgeschwindigkeit in den gewählten natürlichen Einheiten dimensionslos. Damit ergibt sich die Stokes'sche Formel in den gewählten natürlichen Einheiten zu: $$\begin{array}{r}\frac{F}{{\mu }^2/{\rho }_{\mathrm{\infty }}}=3\pi \text{Re}\end{array}$$

Diese ist nun, wie gefordert, eine dimensionslose Größe.

Natürliche Einheiten (Lothar)

Aus den vier System-Parametern $v,R,\rho$ und $\mu$ lassen sich zwei sinnvolle Einheitensätze bilden:

"zähe" Einheiten

Damit ist der Satz $R,\rho$ und $\mu$ gemeint, Basiseinheiten sind $$\rho R^3,R,\frac{R^2}{\rho \mu }$$ für Masse, Länge und Zeit; und $\mu /(\rho R)$ bzw. ${\mu }^2/\rho$ die Geschwindigkeits- bzw. Krafteinheit. Die Reynoldszahl stellt dann gemäß $$\frac{v}{\mu /(\rho R)}=\frac{\text{Re}}{2}$$ die Geschwindigkeit ein, und im Stokes-Regime gilt $$\frac{F}{{\mu }^2/\rho }=3\pi \text{Re}.$$

"träge" Einheiten

Damit ist der Satz $R,v$ und $\rho$ gemeint, Basiseinheiten sind dann $$\rho R^3,R,\frac{R}{v}$$ für Masse, Länge und Zeit; und $\rho vR$ bzw. $\rho v^2{R}^2$ die Viskositäts- bzw. Krafteinheit. Die Reynoldszahl stellt dann gemäß $$\frac{\mu }{\rho vR}=\frac{2}{\text{Re}}$$ die Viskosität ein, und im Stokes-Regime gilt $$\frac{F}{\rho v^2{R}^2}=6\pi \frac{2}{\text{Re}}.$$

NB: Die Zahlenwerte der einheitenbildenden Parameter sind 1 und sollten auch im Code so gewählt werden.

Ergebnisse

Festlegung des Systems für zukünftige Simulationen

Bevor die Simulationen zur Abstimmung der Reynolds-Zahlen durchgeführt werden können, muss zunächst ein geeignetes Setup gefunden werden. Dieses Setup sollte so gewählt werden, dass die Ergebnisse einerseits nicht durch die Wahl des Setups verfälscht werden und andererseits die Simulationsdauer in einem moderaten Rahmen bleibt.

Auflösungsstudie

Es ist zu erwarten, dass die Simulationsdaten und dementsprechend auch die Ergebnisse für sehr grobe Gitter, durch die Wahl des Gitters verfälscht werden können. Daher bietet sich es sich an zunächst Simulationen für feiner aufgelöste Gitter durchzuführen. Das Ziel ist dabei das gröbste Gitter zu finden, für welches die Kraft auf die Kugel sich nicht mehr bzw. kaum ändert. Dafür werden in den entsprechenden Simulationen, Parameter wie die Reynolds-Zahl, die Dichte im Unendlichen, die Schallgeschwindigkeit, etc. konstant gehalten.

Für die erste Simulation dieser Auflösungsstudie wurde ein Gitter mit einem Innenradius $R_I$ von $R_I=1$, welcher dem Radius der angeströmten Kugel entspricht, und einem Außenradius $R_A$ von $R_A=10$ gewählt. Dabei befinden sich zunächst in radialer Richtung $11$, exponentiell mit dem Außenradius größer werdende Zellen. In polarer Richtung befinden sich $15$ Zellen, uniformer Größe. In den nachfolgenden Simulationen wird die Anzahl der Zellen in radialer und polarer Richtung jeweils mit einer natürlichen Zahl $n\in \mathbb{N}$ multipliziert. Dadurch ergibt sich in radialer Richtung eine Zellenanzahl von $n\cdot 11$ und in polarer Richtung eine Zellenanzahl von $n\cdot 15$. Künftig wird das Gitter als ein Gitter mit der Auflösung $n$ bezeichnet.

Die aus den jeweiligen Simulationsdaten ermittelte Kraft $F_{\text{Sim}}$ auf die Kugel wird dann mit der, über die Stokes'schen Formel ermittelte Kraft $F_{\text{Theo}}$ verglichen. Dafür wird die relative Kraftabweichung $\delta F_{\text{rel}}$ betrachtet, welche gegeben ist durch: $$\begin{array}{r}\delta F_{\text{rel}}=\frac{F_{\text{Sim}}-F_{\text{Theo}}}{F_{\text{Theo}}}\end{array}$$

In folgender Abbildung ist die relative Kraftabweichung über die Auflösung des Gitters, für eine Reynolds-Zahl von $\mathrm{Re}={10}^{-2}$, aufgetragen:

Abb.1: Relative Kraftabweichung $\delta F$ aufgetragen über die Gitterauflösung $n$, für ein Gitter mit Außenradius $R_A=10$

Es zeigt sich, dass die aus den jeweiligen Simulationsdaten ermittelte Kraft auch bei zunehmender Auflösung weiterhin um etwa $21,8\mathrm{\%}$ von der über die Stokes'sche Formel berechneten Kraft abweicht. Außerdem fällt auf, dass das Konvergenzverhalten der relativen Kraftabweichung nicht den Erwartungen entspricht. Denn sie fällt zunächst, wie zu erwarten mit steigender Auflösung, bevor sie bei einer Auflösung von $n=4$ ihr Minimum annimmt und dann wieder steigt. Es scheint jedoch so zu sein, dass die relative Kraftabweichung für größere Auflösungen gegen eine Abweichung von ungefähr $22\mathrm{\%}$ konvergiert. Dies widerspricht dabei insoweit den Erwartungen, da eigentlich davon ausgegangen wurde, dass die relative Kraftabweichung, gemäß einer Potenzfunktion, also einer Funktion folgender Form, fällt: $$\begin{array}{r}f(x)=\frac{a}{x^b}+c,\text{mit}a,b,c\in \mathbb{R}\end{array}$$

Dies ist hier jedoch nicht der Fall. Eine mögliche Ursache dafür könnte die endliche Größe des Systems sein, die durch das Gitter begrenzt wird. In der analytischen Herleitung der Stokes'schen Formel wird hingegen angenommen, dass das betrachtete System unendlich ausgedehnt ist. Daher lässt sich die Hypothese aufstellen, dass die vergleichsweise große Abweichung sowie das fragwürdige Konvergenzverhalten durch eine Vergrößerung des Außenradius $R_A$ verringert und das Konvergenzverhalten normalisiert werden könnten.

Um dies zu untersuchen, müssen Simulationen für größere Außenradien bei konstanter Auflösung durchgeführt werden. Dafür ist es notwendig, eine entsprechende Anzahl von Zellen zum Gitter hinzuzufügen, wobei die Breite $\mathrm{\Delta }{x}_i$ der bestehenden Zellen in radialer Richtung beibehalten wird. Die Breite der Zellen wird dabei allgemein durch folgende Formel bestimmt: $$\begin{array}{r}\mathrm{\Delta }{x}_i=(x_{i-\frac{1}{2}}+|x_L|-x_L)({10}^{\mathrm{\Delta }\xi }-1),\text{mit}\mathrm{\Delta }\xi =\frac{1}{N}{\log }_{10}(\frac{x_R+|x_L|-x_L}{|x_L|})\end{array}$$

Dabei entspricht hier $x_{i-\frac{1}{2}}$ den Abständen zum Ursprung an den jeweiligen Zellwänden, $x_L=R_I$ dem Innenradius, $x_R=R_A$ dem Außenradius, und $N$ der Anzahl an Zellen in radialer Richtung.

Damit also die Form der bestehenden Zellen erhalten bleibt muss also die Breite der bestehenden Zellen $\mathrm{\Delta }{x}_{i,n}$ des neuen Gitters, in radialer Richtung gleich der Breite der bestehenden Zellen $\mathrm{\Delta }{x}_{i,a}$ des alten Gitters, in radialer Richtung sein. Es muss also gelten: $$\begin{array}{rl}& \phantom{\leftrightarrow ,}\mathrm{\Delta }{x}_{i,n}=\mathrm{\Delta }{x}_{i,a}\\ & \iff \mathrm{\Delta }{\xi }_n=\mathrm{\Delta }{\xi }_a\\ & \iff N_n=N_v\frac{{\log }_{10}(R_{A,n})}{{\log }_{10}(R_{A,a})},\text{mit}{R}_{A,a}=10\\ & \iff N_n=N_v{\log }_{10}(R_{A,n})\end{array}$$

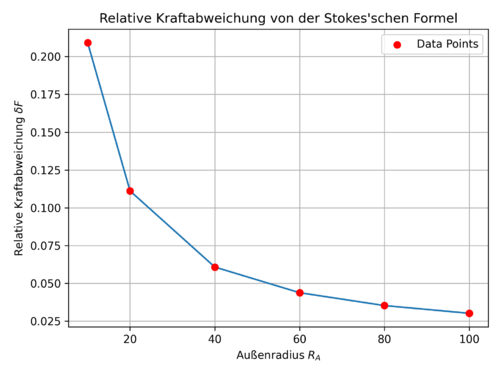
In folgender Abbildung ist die relative Kraftabweichung über den Außenradius des Gitters, für eine Reynolds-Zahl von $\mathrm{Re}={10}^{-2}$ und eine Auflösung von $n=16$, aufgetragen:

Abb.2: Relative Kraftabweichung $\delta F$ aufgetragen über den Außenradius $R_A$ des Gitters, für eine Auflösung von $n=16$

Es lässt sich hierbei erkennen, dass die relative Kraftabweichung mit einem größer werdenden Außenradius kleiner wird und sogar für einen Außenradius von $R_A=100$ auf ungefähr $3\mathrm{\%}$ abfällt. Außerdem fällt auf, dass die relative Kraftabweichung gemäß einer Potenzfunktion, mit dem Außenradius fällt. Dies lässt sich auch anhand folgender doppellogarithmisch dargestellter Abbildung erkennen:

Abb.2: Doppellogarithmische Auftragung der relativen Kraftabweichung $\delta F$ über den Außenradius $R_A$, bei konstanter Auflösung von $n=16$

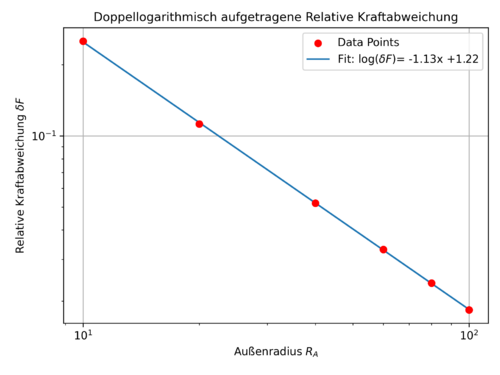
Anhand dieser Simulationsreihe lässt sich bestätigen, dass durch eine Vergrößerung des Außenradius die relative Kraftabweichung geringer wird. Bleibt noch zu klären, ob das fragwürdige Konvergenzverhalten durch die Vergrößerung des Außenradius normalisiert wird. Dafür werden erneut Simulationen für verschiedene Auflösungen, bei einem konstanten Außenradius von $R_A=100$ durchgeführt.

In folgender Abbildung ist die relative Kraftabweichung über die Auflösung des Gitters, für eine Reynolds-Zahl von $\mathrm{Re}={10}^{-2}$, aufgetragen:

\colorbox{yellow}{Plot Kraftabweichung über Auflösung}

In dieser Abbildung lässt sich erkennen, dass sich auch das Konvergenzverhalten, für einen Außenradius von $R_A=100$, normalisiert hat. Die relative Kraftabweichung fällt dabei sogar, mit der Auflösung, gemäß einer Potenzradius. Die lässt sich anhand folgender doppellogarithmisch dargestellter Abbildung erkennen:

\colorbox{yellow}{Plot Kraftabweichung über Auflösung doppellogarithmisch}

Damit lässt sich die aufgestellte Hypothese bestätigen. Denn die vergleichsweise große Abweichung von der Stokes'schen Formel verringert sich und auch das Konvergenzverhalten normalisiert sich, durch das eine Vergrößerung des Außenradius $R_A$.

Analyse der Konvergenzgeschwindigkeit

Da zu erwarten ist, dass die Simulationen einen ähnlichen stationären Zustand erreichen, wie der der analytischen Lösung, lässt sich die Hypothese aufstellen, dass entsprechende Simulationen schneller ihren stationären Zustand erreichen, wenn dem Programm das Druck- und Geschwindigkeitsfeld der analytischen Lösung als Anfangsbedingung übergeben wird, anstelle eines homogenen Druckfeldes und deines Geschwindigkeitsfeldes, welches dem einströmenden Geschwindigkeitsfeld entspricht.

Zur Charakterisierung des Zeitpunktes, ab welcher das jeweilige System stationär ist, wird der zeitliche Verlauf des maximalen Druckes $p_{\mathrm{Max}}$ betrachtet. Dabei muss eine Bedingung an den maximalen Druck im System definiert werden, ab der das System als stationär angenommen werden kann. Im folgenden wird diese Bedingung sein, dass der maximale Druck sich über $15000$ Iterationsschritte maximal um einen Faktor ${10}^{-7}$ zu dem maximalen Druck im vorherigen Iterationsschritt abweichen darf.

Um nun Untersuchen zu können, ob das System schneller seinen stationären Zustand erreicht, wenn die Simulationen aus der analytischen Lösung gestartet werden, wird eine Simulationsreihe, mit einem veränderlichen Außenradius, bei fester Auflösung von $n=16$ durchgeführt. Diese Simulationen werden dann mit der entsprechenden Simulationsreihe verglichen, dessen Simulationen mit dem homogenen Druckfeld und dem einstrahlenden Geschwindigkeitsfeld gestartet werden.

In folgender sind dann die maximalen Drücke in Abhängigkeit von der Zeit für die verschiedenen Anfangsbedingungen und Außenradien, bei einer Reynolds-Zahl von $\mathrm{Re}={10}^{-2}$ und einer Auflösung von $n=16$ aufgetragen:

\colorbox{yellow}{Subplots maximale Drücke über Zeit}

Dabei lässt sich erkennen, dass die Simulationen, welche aus der analytischen Lösung gestartet werden, ihren stationären Zustand etwas früher erreichen. Dies lässt sich auch an folgender Abbildung erkennen, in der die Zeitpunkte $t_{\mathrm{stat}}$, ab denen das System in den stationären Zustand übergeht, in Abhängigkeit vom jeweiligen Außenradius des Systems dargestellt sind:

\colorbox{yellow}{Plot Zeitpunkt, ab der System stationär, über Außenradius}

Damit lässt sich die aufgestellte Hypothese prinzipiell bestätigen. Allerdings führt das Starten der Simulationen aus der analytischen Lösung nicht zu der erwarteten Zeitersparnis. Die Simulationen erreichen den stationären Zustand für die jeweiligen Außenradien nahezu gleichzeitig, verglichen zur gesamten Simulationszeit.