Windtunnel/Boundary Conditions
Jump to navigation
Jump to search
New Keywords
in pluto.ini
ObjectType_int: 0=nothing, 1=cylinder/sphere, 2=square/cube of sizeObjectDiameter_cmWindPressure_Pa,WindPressure_mbar(mutually exclusive): pressure at entry (left)PressureGradient_mbar_per_cmpositive (even though pressure drops from left to right)- Wind velocity is ramped up to
WindVelocity_m_per_sover timeInjectionTime_s WindTemperature_CKinematicViscosity_m2_per_s,DynamicViscosity_Pa_s,Wall_BoundaryConditionfor tangential walls, value from {0,1,2,3}
(ignored if given values <0)
in init.c
- macro
SOLIDto enable an object - array
solidcontaining value 1 or 0 for object matter being present/absent
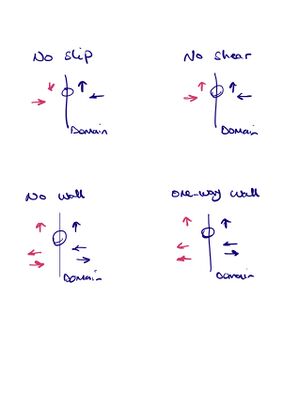
Walls
tangential
| Boundary condition for the wall | ||
|---|---|---|
| vx1 | vx2 | |
| no-shear | zero-gradient | reflective |
| no-slip | reflective | reflective |
| no-wall | zero-gradient | zero-gradient |
| one-way wall | zero-gradient | zero-gradient & no-inflow |
entry/exit
prescribed velocity at entry (left)
prescribe pressure drop (left to right)
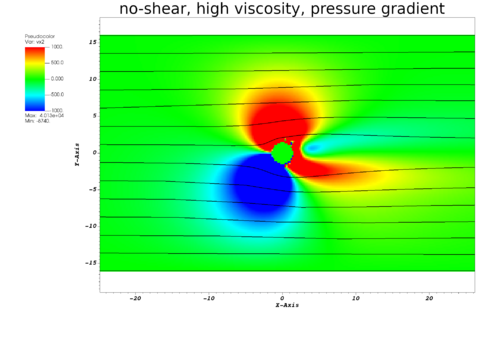
- current simulation result: \(v_x\)-profile slightly asymmetric and \(v_x<0\) at one wall
Object
- Strong asymmetry when driven by pressure gradient. Bug!
- At the boundary of a region which has
FLAG_INTERNAL_BOUNDARYset, no boundary conditions are specified. Ghostcells are frozen.
Open Questions
Reflective cells
Setting the vector \(\vec v_g\) in a ghost cell as \(\vec v_g=-\vec v\), with \(\vec v\) being the value in the adjacent real cell, yields \(\vec 0\) as interpolation right at the boundary. This works for plane walls. What to do in cases where a ghost cell has more than one real cell as nearest neighbor? This calls for discussion!
Analytical Solutions
empty 2D channel
$$ v_x(y) = \frac{\Delta p}{L}\frac{D^2/4-y^2}{2\mu} $$
empty circular tube
$$ v_z(r) = \frac{\Delta p}{L}\frac{R^2-r^2}{4\mu} $$
with \(\mu\)=dynamical viscosity