BA Lena Schürmann: Difference between revisions
Jump to navigation
Jump to search
m (Added experimental data) |
(→Über erste Periodendauer:: Plots ergänzt) |
||
| Line 5: | Line 5: | ||
==== Literaturdaten: ==== | ==== Literaturdaten: ==== | ||
Zusammentragung von Daten in M.M Zdrakowich's Volume 1: Flow around circular cylinders: | Zusammentragung von Daten in M.M Zdrakowich's Volume 1: Flow around circular cylinders: | ||
[[File:Experimentelle Daten zum Fluss um einen Zylinder.png | [[File:Experimentelle Daten zum Fluss um einen Zylinder.png|thumb|Zusammentragung von experimentellen Daten aus M.M. Zdrakovich Volume 1: Flow Around Cyrcular Cylinders. Auftragung der Strouhal-Zahl (Ablösefrequenz der Wirbel einer von Karman-Straße) über die Reynolds-Zahl]] | ||
==== Methode 1: Analyse mittels Autokorrelation: ==== | ==== Methode 1: Analyse mittels Autokorrelation: ==== | ||
| Line 25: | Line 25: | ||
File:Index.php?title=File:Re100 Autokorr.png|bei [https://de.wikipedia.org/wiki/Reynolds-Zahl Reynolds-Zahl] 100 und [https://de.wikipedia.org/wiki/Mach-Zahl Mach-Zahl] 0.01 | File:Index.php?title=File:Re100 Autokorr.png|bei [https://de.wikipedia.org/wiki/Reynolds-Zahl Reynolds-Zahl] 100 und [https://de.wikipedia.org/wiki/Mach-Zahl Mach-Zahl] 0.01 | ||
</gallery> | </gallery> | ||
[[File:St Re Autokorr T0.png|thumb|Auftragung der Strouhal-Zahl errechnet aus der Periodendauer des ersten signifikaten Peaks der Autokorrelationsfunktion. Mittlung über alle Zellen der Simulation, Fehlerbalken entsprechen der Standardabweichung]] | |||
===== Über erste Periodendauer: ===== | ===== Über erste Periodendauer: ===== | ||
| Line 38: | Line 39: | ||
return diffs_mod*stepwidth | return diffs_mod*stepwidth | ||
</syntaxhighlight> | </syntaxhighlight> | ||
[[File:St Re Autokorr.png|thumb|Auftragung der Strouhal-Zahl errechnet aus den mittleren Abständen der Peaks der Autokorrelationsfunktion. Mittlung über alle Zellen der Simulation, Fehlerbalken entsprechen der Standardabweichung]] | |||
===== Über Durchschnittliche Periodendauer: ===== | ===== Über Durchschnittliche Periodendauer: ===== | ||
| Line 52: | Line 54: | ||
return diffs_mod*stepwidth | return diffs_mod*stepwidth | ||
</syntaxhighlight> | </syntaxhighlight> | ||
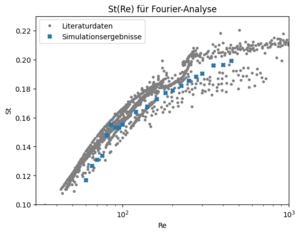
[[File:St Re Fourier.png|thumb|Auftragung der Strouhal-Zahl errechnet aus den mittleren Peak-Abständen der Fourier-Transformierten aller Zellen der Simulation und der Observablen Druck, Dichte und Geschwindigkeit.]] | |||
==== Methode 2: Analyse mittels Fourier-Analyse: ==== | ==== Methode 2: Analyse mittels Fourier-Analyse: ==== | ||
Revision as of 08:36, 21 June 2024
Vortragstitel im Bachelorseminar: Modellierung und Analyse der Ablösefrequenz von von Kármán-Straßen
Analyse der Ablösefrequenz:
Literaturdaten:
Zusammentragung von Daten in M.M Zdrakowich's Volume 1: Flow around circular cylinders:
Methode 1: Analyse mittels Autokorrelation:
Hier wird die Autokorrelationsfunktion in ihrer allgemeinen normierten Form verwendet. Es stellt sich heraus, dass eine Periode der Autokorrelationsfunktion der Tangentialgeschwindigkeit mit der Periode der Wirbelablösung übereinstimmt. Im Fall der anderen Größen ist die Periode in der Regel kleiner.
def cov(a,b):
return np.mean(np.dot((a-np.mean(a)),(b-np.mean(b))))
def autokorr(data):
autok=[]
for tau in range (0,int(len(data))):
data_a=data[:len(data)-tau]
data_b=data[tau:]
temp=cov(data_a,data_b)/np.sqrt(cov(data_a,data_a)*cov(data_b,data_b))
autok.append(temp)
autok=np.asarray(autok)
return autok
- Autokorrelationsfunktion (Verallgemeinerung) angewandt auf die Zeitreihen von Druck, Dichte und Geschwindigkeit an Position r=12,42 und phi=180° hinter einem Zylinder. Maximalstellen markiert durch x kennzeichnen lokal höchste Übereinstimmung der Zeitreihen. Literaturwert als grobe visuelle Orientierung (umgerechnet in Perioden aus Daten von Roshko).
bei Reynolds-Zahl 60 und Mach-Zahl 0.01
- Index.php?title=File:Re100 Autokorr.png
bei Reynolds-Zahl 100 und Mach-Zahl 0.01
Über erste Periodendauer:
def autokorr_mod(vs_r, mesh_grid,stepwidth):
phis_min=0
phis_max=np.shape(mesh_grid)[1]
diffs_mod=[]
for rs in range (0,np.shape(mesh_grid)[0]):
for phi in range (phis_min,phis_max):
diffs_mod.append(np.asarray(sp.find_peaks(autokorr(vs_r[:,rs,phi]))[0])[0])
return diffs_mod*stepwidth
Über Durchschnittliche Periodendauer:
def autokorr_anw_mod(vs_r, mesh_grid,stepwidth):
phis_min=0
phis_max=np.shape(mesh_grid)[1]
diffs_mod=[]
for rs in range (0,np.shape(mesh_grid)[0]):
for phi in range (phis_min,phis_max):
vs_auto_maxs=np.asarray(sp.find_peaks(autokorr(vs_r[:,rs,phi]))[0])
diffs_mod=np.hstack((diffs_mod,(vs_auto_maxs[1:]-vs_auto_maxs[:-1])[0]))
return diffs_mod*stepwidth