Windtunnel/Boundary Conditions: Difference between revisions
Jump to navigation
Jump to search
m (→empty 2D channel: 1/2) |
(→Object: flux 0) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 48: | Line 48: | ||
* current simulation result: | * current simulation result: | ||
= Object = | = Object = | ||
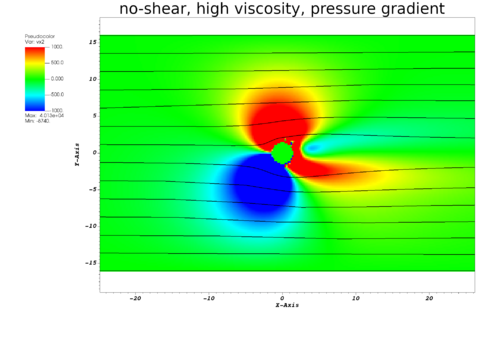
* Strong asymmetry when driven by pressure gradient. Bug! | |||
[[File:Asymmetry.png|thumb|center|500px| | |||
* At the boundary of a region which has <code>FLAG_INTERNAL_BOUNDARY</code> set, '''no''' boundary conditions are specified. Ghostcells are frozen. | |||
* Rolfs proposition for the object boundary: Set the mass ''flux'' at the boundary to zero after the Riemann solver has computed it. | |||
= Open Questions = | = Open Questions = | ||
| Line 62: | Line 68: | ||
$$ | $$ | ||
v_x(y) = \frac{\Delta p}{L}\frac{D^2/4-y^2}{2\mu} | |||
$$ | $$ | ||
| Line 68: | Line 74: | ||
$$ | $$ | ||
v_z(r) = \frac{\Delta p}{L}\frac{R^2-r^2}{4\mu} | |||
$$ | $$ | ||
with | with | ||
Latest revision as of 15:48, 29 October 2024
New Keywords
in pluto.ini
ObjectType_int: 0=nothing, 1=cylinder/sphere, 2=square/cube of sizeObjectDiameter_cmWindPressure_Pa,WindPressure_mbar(mutually exclusive): pressure at entry (left)PressureGradient_mbar_per_cmpositive (even though pressure drops from left to right)- Wind velocity is ramped up to
WindVelocity_m_per_sover timeInjectionTime_s WindTemperature_CKinematicViscosity_m2_per_s,DynamicViscosity_Pa_s,Wall_BoundaryConditionfor tangential walls, value from {0,1,2,3}
(ignored if given values <0)
in init.c
- macro
SOLIDto enable an object - array
solidcontaining value 1 or 0 for object matter being present/absent
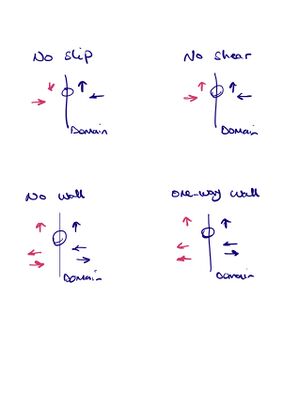
Walls
tangential
| Boundary condition for the wall | ||
|---|---|---|
| vx1 | vx2 | |
| no-shear | zero-gradient | reflective |
| no-slip | reflective | reflective |
| no-wall | zero-gradient | zero-gradient |
| one-way wall | zero-gradient | zero-gradient & no-inflow |
entry/exit
prescribed velocity at entry (left)
prescribe pressure drop (left to right)
- current simulation result:
Object
- Strong asymmetry when driven by pressure gradient. Bug!
- At the boundary of a region which has
FLAG_INTERNAL_BOUNDARYset, no boundary conditions are specified. Ghostcells are frozen. - Rolfs proposition for the object boundary: Set the mass flux at the boundary to zero after the Riemann solver has computed it.
Open Questions
Reflective cells
Setting the vector
Analytical Solutions
empty 2D channel
empty circular tube
with